Question

In two concentric circles, prove that all chords of the outer circle which touch the inner circle are of equal length.

Answer 1

Hint: Take two lines as chords of larger circle as tangents of smaller circle. Try to prove they are equal using the theorem if two chords are equidistant from the centre they are equal to each other.

Complete step-by-step answer:
In the question it is given that there are two concentric circles and we have to prove that all chords of outer circle touch the inner circle are of equal length.
So, we know concentric circles are the circles with the same centre but different radii.
In other words we can say that two or more circles that have the same centre and different radii are known as concentric circles.

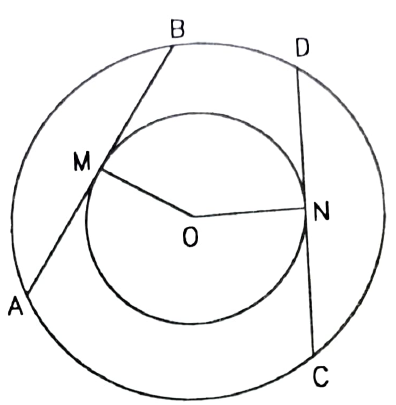
Let us suppose that AB and CD are two chords of the larger circle which touches the inner circle at M and N, respectively.
So in this we have to prove that chords AB and CD are equal.
Now as we know that AB and CD are the tangents to the smaller circle.
Then lengths of OM and ON are equal as they are the radius of the smaller circle and the radius is even throughout the circle.
As AB and CD are chords of a bigger circle and are equidistant from the centre,so AB = CD.
Hence in two concentric circles, all chords of the outer circle which touch the inner circle are of equal length.
Hence proved.

Note: Students should be familiar with the terms like concentric circles and also the properties of circles. They should know about the theorems related to the circle.
Another approach to solve this is, considering triangles OMB and OND. They are right angled triangles, so apply Pythagoras theorem and find out the value of BM and DN.

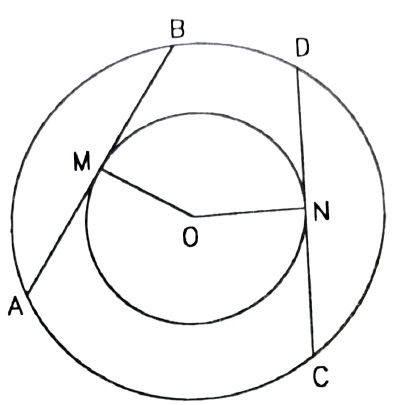
Similarly, consider triangles AMO and CNO. They are also right angled triangles, so apply Pythagoras theorem and find out the value of AM and CN.
Then find out the value of AB and CD prove the desired result.