Question

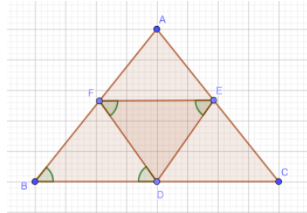
In $\triangle$ABC, BDEF and FDCE are parallelograms. Which of the following is correct?

$\left(a\right)$AB=EF
$\left(b\right)$DB=AB
$\left(c\right)$ED$\neq$BF
$\left(d\right)$BD=CD

Answer 1

Hint: We are given a diagram here in which there are two parallelograms as stated in the question. We are going to use the property of parallelogram that the opposite sides of a parallelogram are parallel and equal to each other. After using that we will tick the correct option out of the given four options. You need to be aware about the properties of a parallelogram for this question to be done correctly.

Complete step by step answer:
We have the following figure given in the question:

Note here that BDEF is a parallelogram. So, using the property of parallelogram that the opposite sides of a parallelogram are equal, we can write the fact that:
FE is parallel to BD and also it can be said that:
FE=BD…………$\left(1\right)$
Now, FDCE is also a parallelogram. So again using the same property, we can say that:
FE is parallel to CD and also we can say that:
FE=CD…………$\left(2\right)$
From$\left(1\right)$and$\left(2\right)$, we can say that
BD=CD.
Looking at the options we find that it matches option $\left(d\right)$.
So, the correct answer is “Option d”.

Note: Do not look directly at the figure and then point out the correct option. You cannot just look at a line segment and assume its length to be equal to that of any other line segment. Always prove the results in a concrete manner first then tick the correct option. Moreover, the basic properties of a parallelogram should always be kept in mind and using those you can figure out the correct answer by yourself.