Question

In triangle ABC; AB=AC and D is a point in BC then, BD=AD.
AD is parallel to BC.
If the above statement is true then mention the answer as 1, else mention 0 if false.

Answer 1

Hint: This question is from the topic of triangles. We are going to use the SAS rule here to solve this question. We will use the CPCT theorem here. CPCT theorem states that if two triangles are taken and are congruent to each other, then the corresponding sides and angles of the triangles are also congruent to each other. First, we will make the two triangles congruent. After that, we will check if AD is parallel to BC.

Complete step by step answer:
Let us solve this question.
In this question, we have given a triangle ABC in which the side AB is equal to the side AC. And, it is also given that there is a point D on the line BC, which says that the side BD is equal to the side AD.
We can take reference from the following figure.

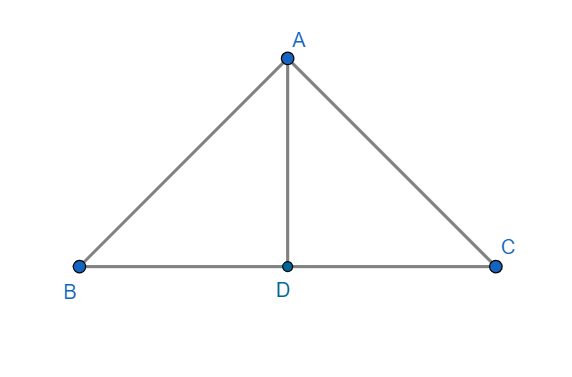
In this triangle, we have to check if AD is parallel to BD or not.
It is a theorem that the two angles of a triangle are equal, if opposite sides of them are equal.
Then, we can say from the triangle ABC that \[\angle \text{ABC=}\angle \text{ACB}\] because opposite sides of these angles are equal (that is AB=AC) which is given in the question
Now, let us check if the triangles ABD and ACD are congruent or not.
In the triangles ABD and ACD, we can write
AD=AD (they are common)
AB=AC (given in the question)
\[\angle \text{ABC=}\angle \text{ACB}\] (As we have seen above)
Now, we can see that two sides and one angle of the triangle are equal. So, according to the SAS rule, the triangle ABD and triangle ACD are congruent.
Now, by CPCT rule, we can say that
\[\angle \text{ADB=}\angle \text{ADC}\]
Using the formula for angles on straight line, we can write
\[\angle \text{ADB+}\angle \text{ADC=180}{}^\circ \]
As we have proved above that\[\angle \text{ADB=}\angle \text{ADC}\], so we can write the above equation as
\[\Rightarrow \angle \text{ADB+}\angle \text{ADB=180}{}^\circ \]
The above equation can also be written as
\[\Rightarrow 2\angle \text{ADB=180}{}^\circ \]
Now, dividing the equation by 2 on both sides of equation, we get
 \[\Rightarrow \angle \text{ADB=90}{}^\circ \]
From here, we can see that AD is perpendicular to BC as it is 90 degrees and we can say that AD is not parallel to BC. So, the station is false.

So, the correct answer is “0”.

Note: We should have better knowledge in trigonometry. We should know how to check if two triangles are congruent or not. Remember the SAS rule. This rule says that two triangles are congruent if any two sides and an angle of one triangle is equivalent to the corresponding two sides and an angle of another triangle. We should know about CPCT rule. CPCT stands for Corresponding Parts of Congruent Triangles. We have used the CPCT rule in the solution and understood about it in the hint. Always remember that the sum of angles of a straight line at a point is 180 degrees.