Question

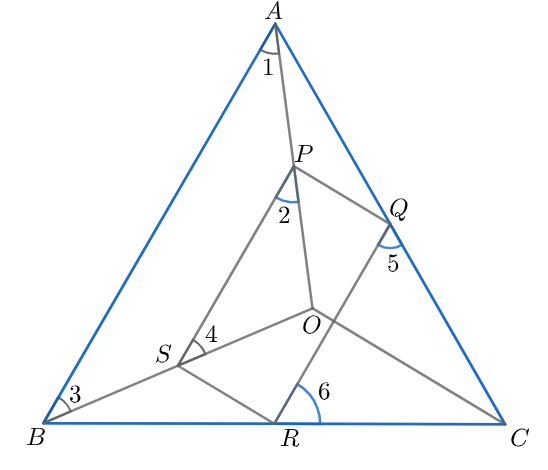
In the given figure, if PQRS is a parallelogram and \[AB||PS\] , then prove that \[OC||SR\] .

Answer 1

Hint: Problems related to triangles and parallelograms are a bit tricky to understand, but can be solved very easily if we get all the key concepts behind the problem. We need to be fluent with some basic as well as some advanced topics of triangles, parallelograms, similarity of triangles and their various properties. A parallelogram is a closed bounded figure consisting of four sides, in which opposite sides are equal and are parallel to one another. The lines which are marked with an arrow, are parallel to one another.

Complete step by step answer:
Now we start off with the solution to the given problem. In the triangles \[OAB\text{ and }OPS\] , we have \[AB||PS\] and \[\angle 1=\angle 2\] and \[\angle 3=\angle 4\] . Thus we can say triangles \[OAB\text{ and }OPS\] are similar. We can write,
\[\dfrac{OP}{OA}=\dfrac{OS}{OB}=\dfrac{PS}{AB}.......\left( i \right)\]
We have \[AB||PS||QR\] . Now in triangles \[CQR\text{ and }CAB\] , we have \[AB||QR\] and \[\angle 1=\angle 2\] and \[\angle 3=\angle 4\] . Now we can say that the triangles \[CQR\text{ and }CAB\] are similar to one another. We can then write,
 \[\dfrac{CQ}{CA}=\dfrac{CR}{CB}=\dfrac{QR}{AB}.......\left( ii \right)\]
We can also write,
\[\dfrac{PS}{AB}=\dfrac{CR}{CB}=\dfrac{CQ}{CA}.......\left( iii \right)\]
\[\Rightarrow \dfrac{CR}{CB}=\dfrac{OS}{OB}.......\left( iv \right)\] from the equations (i) and (iii)
From the above relation that we have, we can say this equation holds good for triangles \[BOC\] . Now from the intermediate equation we can say that \[OC||SR\] .

Note: While solving problems like these we need to be very careful in choosing the triangles where we apply our similarity theorem or else it may result in a wrong solution. We also need to have some previous background knowledge of triangles, parallelograms and similarity. The properties of triangles, parallelograms and other polygonal figures should also be revised before solving the problem.