Question

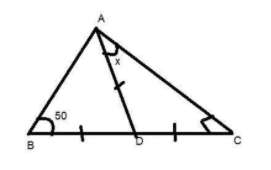
In the given figure, find the value of x.
${\text{A}}{\text{. }}{40^0}$
${\text{B}}{\text{. }}{50^0}$
${\text{C}}{\text{. }}{60^0}$
${\text{D}}{\text{. }}{25^0}$

Answer 1

Hint: Here we go through the properties of the isosceles triangle and the properties of the sum of all internal angles of a triangle which is ${180^0}$ to find the unknown angle.

Given that ABC is a triangle in which D is the midpoint of side BC.
So we can say that BD=DC.
It is also given that the length AD is equal to the length BD and DC.
$\therefore {\text{AD = BD = DC}}$
Now in $\vartriangle {\text{ABD}}$
${\text{AD = BD}}$ (Given in the question)
It means that $\vartriangle {\text{ABD}}$ is an isosceles triangle.
So the base angle of side BD and AD are equal which means $\angle {\text{DBA = }}\angle {\text{DAB = 5}}{{\text{0}}^0}$ given in the figure.
And we know that the sum of all interior angles of a triangle is ${180^0}$.
$
  \therefore \angle {\text{DBA + }}\angle {\text{DAB + }}\angle {\text{BDA}} = {180^0} \\
   \Rightarrow {50^0} + {50^0} + \angle {\text{BDA}} = {180^0} \\
   \Rightarrow \angle {\text{BDA}} = {180^0} - {100^0} \\
  \therefore \angle {\text{BDA}} = {80^0} \\
$
And now BDC is a straight line
$\therefore \angle {\text{BDA}} + \angle {\text{ADC = 18}}{{\text{0}}^0}$ Straight angle.
$ \Rightarrow \angle {\text{ADC = 18}}{{\text{0}}^0} - {80^0} = {100^0}$ $\because \angle {\text{BDA}} = {80^0}$
And now in $\vartriangle {\text{ABC}}$
${\text{AD = CD}}$ (Given in question).
It means that $\vartriangle {\text{ADC}}$ is an isosceles triangle.
So the base angle of side BD and AD are equal which means $\angle {\text{DCA = }}\angle {\text{DAC = }}x$ given in the figure.
And we know that the sum of all interior angles of a triangle is ${180^0}$.
$
  \therefore \angle {\text{DCA + }}\angle {\text{DAC + }}\angle {\text{ADC}} = {180^0} \\
   \Rightarrow x + x + {100^0} = {180^0} \\
   \Rightarrow 2x = {180^0} - {100^0} \\
  \therefore x = {40^0} \\
$
Hence, option A is the correct answer.

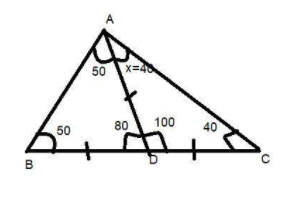
Note: Whenever we face such a type of question the key concept for solving the question is that you have to first read the diagram what it says and the data which are given in the diagrams. Then by applying the properties of triangles start finding the unknown terms to get the answer.