
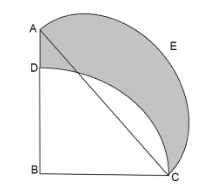
In the given figure, find the area of the shaded region and also its perimeter if the length of AB and BC (in cm) is 28 and 21 respectively and BCD is a quadrant of circle. AEC is semicircle on AC as diameter (Take\[\pi = \dfrac{{22}}{7}\])

Answer
561.3k+ views
Hint: We find the area of quadrant using the length of the radius of the quadrant. Calculate the area of the triangle ABC which has one angle as the right angle. Use Pythagoras theorem to calculate the value of AC and use that length as diameter of semicircle. Calculate radius by dividing diameter into half and find the area of semicircle. Shaded region is given by subtracting the area of quadrant from sum of areas of semicircle and triangle. Calculate the perimeter by adding the length of curve of quadrant, semicircle and the length AD.
* Area of the circle with radius ‘r’ is\[\pi {r^2}\]. A quadrant of a circle means one-fourth of the circle, so the area of the quadrant will be \[\dfrac{{\pi {r^2}}}{4}\]. Similarly semicircle means half of the circle, so the area of semicircle will be \[\dfrac{{\pi {r^2}}}{2}\].
* Area of any triangle is given by \[\dfrac{1}{2} \times \]Base\[ \times \]Height
* Pythagoras theorem states that in a right angled triangle, the sum of square of base and square of height is equal to square of the hypotenuse. In the right triangle the largest side opposite to the right angle is the hypotenuse.
If we have a right angled triangle, \[\vartriangle ABC\] with right angle, \[\angle B = {90^ \circ }\]
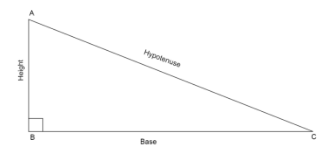
Then using the Pythagoras theorem we can write that \[A{C^2} = A{B^2} + B{C^2}\]
* Circumference of a circle with radius ‘r’ is \[2\pi r\].
* Perimeter of any figure is the total length of the outline of that figure.
Complete step-by-step solution:
The figure consists of a quadrant, a semicircle and a right angled triangle.
We find the area of each figure separately.
(i) Quadrant:
Quadrant is one-fourth part of the circle.
In the given figure, the quadrant BCD has radius \[BC = BD = 21\]cm
Since we know area of quadrant having radius ‘r’ is given by \[\dfrac{{\pi {r^2}}}{4}\]
\[ \Rightarrow \]Area of quadrant BCD \[ = \dfrac{{\pi {{(21)}^2}}}{4}\]
Substitute the value of \[\pi = \dfrac{{22}}{7}\]
\[ \Rightarrow \]Area of quadrant BCD \[ = \dfrac{{22}}{7} \times \dfrac{{21 \times 21}}{4}\]
Cancel same factors from numerator and denominator
\[ \Rightarrow \]Area of quadrant BCD \[ = \dfrac{{11 \times 3 \times 21}}{2}\]
\[ \Rightarrow \]Area of quadrant BCD \[ = \dfrac{{693}}{2}\]
\[ \Rightarrow \]Area of quadrant BCD \[ = 346.5\]\[c{m^2}\].....................… (1)
(ii) Triangle:
In the given figure, the right angle triangle is\[\vartriangle ABC\]with base BC and height AB.
Since we know area of any triangle is given by \[\dfrac{1}{2} \times \]Base\[ \times \]Height
\[ \Rightarrow \] Area of\[\vartriangle ABC = \dfrac{1}{2} \times BC \times AB\]
Substitute the values of BC and AB
\[ \Rightarrow \] Area of\[\vartriangle ABC = \left( {\dfrac{1}{2} \times 21 \times 28} \right)\]\[c{m^2}\]
Cancel same factors from numerator and denominator
\[ \Rightarrow \] Area of\[\vartriangle ABC = \left( {21 \times 14} \right)\]\[c{m^2}\]
\[ \Rightarrow \] Area of\[\vartriangle ABC = 294\]\[c{m^2}\]......................… (2)
In right triangle\[\vartriangle ABC,\angle B = {90^ \circ }\]
Use Pythagoras theorem to find the length of hypotenuse AC
\[ \Rightarrow A{C^2} = A{B^2} + B{C^2}\]
Substitute the values of \[AB = 28,BC = 21\]
\[ \Rightarrow A{C^2} = {(28)^2} + {(21)^2}\]
\[ \Rightarrow A{C^2} = 784 + 441\]
\[ \Rightarrow A{C^2} = 1225\]
We can write \[1225 = {(35)^2}\]
\[ \Rightarrow A{C^2} = {(35)^2}\]
Take under root on both sides of the equation
\[ \Rightarrow \sqrt {A{C^2}} = \sqrt {{{(35)}^2}} \]
Cancel square root by square power on both sides
\[ \Rightarrow AC = 35\]..................… (3)
(iii) Semicircle:
In the given figure, semicircle is AEC
Diameter of the semicircle is AC
Since radius of semicircle is half the diameter of the semicircle
\[ \Rightarrow r = \dfrac{{AC}}{2}\]
\[ \Rightarrow r = \dfrac{{35}}{2}\]cm
Since we know area of semicircle having radius ‘r’ is given by \[\dfrac{{\pi {r^2}}}{2}\]
\[ \Rightarrow \]Area of semicircle AEC \[ = \dfrac{\pi }{2} \times {\left( {\dfrac{{35}}{2}} \right)^2}\]
Substitute the value of\[\pi = \dfrac{{22}}{7}\]
\[ \Rightarrow \]Area of semicircle AEC \[ = \dfrac{{22}}{{7 \times 2}} \times \dfrac{{35 \times 35}}{{2 \times 2}}\]
Cancel same factors from numerator and denominator
\[ \Rightarrow \]Area of semicircle AEC \[ = \left( {\dfrac{{11 \times 5 \times 35}}{{2 \times 2}}} \right)\]\[c{m^2}\]
\[ \Rightarrow \]Area of semicircle AEC \[ = \left( {\dfrac{{1925}}{4}} \right)\]\[c{m^2}\]
\[ \Rightarrow \]Area of semicircle AEC \[ = 481.25\]\[c{m^2}\]...................… (4)
We know the shaded region is given by subtracting the area of the quadrant from the sum of areas of semicircle and triangle.
Area of shaded area is given by subtracting equation (1) from sum of equations (2) and (4)
\[ \Rightarrow \]Area of shaded region \[ = (481.25 + 294) - (346.5)\]\[c{m^2}\]
\[ \Rightarrow \]Area of shaded region \[ = 428.75\]\[c{m^2}\]
\[\therefore \]Area of shaded region is\[428.75\]\[c{m^2}\]
Now we have to calculate the perimeter of the shaded region.
Perimeter of the shaded region has circumference of the quadrant, circumference of the semicircle and the line AD.
(i) Quadrant:
Circumference of quadrant \[ = \dfrac{{2\pi r}}{4}\]
Here value of \[r = 21\]as \[BC = 21\]cm
\[ \Rightarrow \]Circumference of quadrant \[ = \left( {2 \times \dfrac{{22}}{7} \times \dfrac{{21}}{4}} \right)\]cm
Cancel same factors from numerator and denominator
\[ \Rightarrow \]Circumference of quadrant \[ = \left( {11 \times 3} \right)\]cm
\[ \Rightarrow \]Circumference of quadrant \[ = 33\]cm………………….… (5)
(ii) Semicircle:
Circumference of semicircle \[ = \dfrac{{2\pi r}}{2}\]
\[ \Rightarrow \]Circumference of semicircle \[ = \pi r\]
Here value of \[r = \dfrac{{35}}{2}\]as \[AC = 35\]cm is the diameter of the semicircle
\[ \Rightarrow \]Circumference of semicircle \[ = \left( {\dfrac{{22}}{7} \times \dfrac{{35}}{2}} \right)\]cm
Cancel same factors from numerator and denominator
\[ \Rightarrow \]Circumference of semicircle \[ = \left( {11 \times 5} \right)\]cm
\[ \Rightarrow \]Circumference of semicircle \[ = 55\]cm……………….… (6)
(iii) AD:
We know \[AD = AB - BD\]
Substitute the value of \[AB = 28;BD = 21\]
\[ \Rightarrow AD = \left( {28 - 21} \right)\]cm
\[ \Rightarrow AD = 7\]cm…………...… (7)
So, the perimeter of the shaded area is sum of equations (5), (6) and (7)
\[ \Rightarrow \]Perimeter \[ = (33 + 55 + 7)\]cm
\[ \Rightarrow \]Perimeter \[ = 95\]cm
\[\therefore \]Perimeter of the shaded region is 95cm.
Note: Students are likely to make the mistake of calculating the perimeter wrong as they add the complete perimeter of the quadrant and the semicircle and add them. Keep in mind the radius of both semicircles and the quadrant plays no role in the perimeter of the shaded area. Perimeter is the boundary of the shaded region and that is made up of the part of circumferences of the quadrant and semicircle.
* Area of the circle with radius ‘r’ is\[\pi {r^2}\]. A quadrant of a circle means one-fourth of the circle, so the area of the quadrant will be \[\dfrac{{\pi {r^2}}}{4}\]. Similarly semicircle means half of the circle, so the area of semicircle will be \[\dfrac{{\pi {r^2}}}{2}\].
* Area of any triangle is given by \[\dfrac{1}{2} \times \]Base\[ \times \]Height
* Pythagoras theorem states that in a right angled triangle, the sum of square of base and square of height is equal to square of the hypotenuse. In the right triangle the largest side opposite to the right angle is the hypotenuse.
If we have a right angled triangle, \[\vartriangle ABC\] with right angle, \[\angle B = {90^ \circ }\]

Then using the Pythagoras theorem we can write that \[A{C^2} = A{B^2} + B{C^2}\]
* Circumference of a circle with radius ‘r’ is \[2\pi r\].
* Perimeter of any figure is the total length of the outline of that figure.
Complete step-by-step solution:
The figure consists of a quadrant, a semicircle and a right angled triangle.
We find the area of each figure separately.
(i) Quadrant:
Quadrant is one-fourth part of the circle.
In the given figure, the quadrant BCD has radius \[BC = BD = 21\]cm
Since we know area of quadrant having radius ‘r’ is given by \[\dfrac{{\pi {r^2}}}{4}\]
\[ \Rightarrow \]Area of quadrant BCD \[ = \dfrac{{\pi {{(21)}^2}}}{4}\]
Substitute the value of \[\pi = \dfrac{{22}}{7}\]
\[ \Rightarrow \]Area of quadrant BCD \[ = \dfrac{{22}}{7} \times \dfrac{{21 \times 21}}{4}\]
Cancel same factors from numerator and denominator
\[ \Rightarrow \]Area of quadrant BCD \[ = \dfrac{{11 \times 3 \times 21}}{2}\]
\[ \Rightarrow \]Area of quadrant BCD \[ = \dfrac{{693}}{2}\]
\[ \Rightarrow \]Area of quadrant BCD \[ = 346.5\]\[c{m^2}\].....................… (1)
(ii) Triangle:
In the given figure, the right angle triangle is\[\vartriangle ABC\]with base BC and height AB.
Since we know area of any triangle is given by \[\dfrac{1}{2} \times \]Base\[ \times \]Height
\[ \Rightarrow \] Area of\[\vartriangle ABC = \dfrac{1}{2} \times BC \times AB\]
Substitute the values of BC and AB
\[ \Rightarrow \] Area of\[\vartriangle ABC = \left( {\dfrac{1}{2} \times 21 \times 28} \right)\]\[c{m^2}\]
Cancel same factors from numerator and denominator
\[ \Rightarrow \] Area of\[\vartriangle ABC = \left( {21 \times 14} \right)\]\[c{m^2}\]
\[ \Rightarrow \] Area of\[\vartriangle ABC = 294\]\[c{m^2}\]......................… (2)
In right triangle\[\vartriangle ABC,\angle B = {90^ \circ }\]
Use Pythagoras theorem to find the length of hypotenuse AC
\[ \Rightarrow A{C^2} = A{B^2} + B{C^2}\]
Substitute the values of \[AB = 28,BC = 21\]
\[ \Rightarrow A{C^2} = {(28)^2} + {(21)^2}\]
\[ \Rightarrow A{C^2} = 784 + 441\]
\[ \Rightarrow A{C^2} = 1225\]
We can write \[1225 = {(35)^2}\]
\[ \Rightarrow A{C^2} = {(35)^2}\]
Take under root on both sides of the equation
\[ \Rightarrow \sqrt {A{C^2}} = \sqrt {{{(35)}^2}} \]
Cancel square root by square power on both sides
\[ \Rightarrow AC = 35\]..................… (3)
(iii) Semicircle:
In the given figure, semicircle is AEC
Diameter of the semicircle is AC
Since radius of semicircle is half the diameter of the semicircle
\[ \Rightarrow r = \dfrac{{AC}}{2}\]
\[ \Rightarrow r = \dfrac{{35}}{2}\]cm
Since we know area of semicircle having radius ‘r’ is given by \[\dfrac{{\pi {r^2}}}{2}\]
\[ \Rightarrow \]Area of semicircle AEC \[ = \dfrac{\pi }{2} \times {\left( {\dfrac{{35}}{2}} \right)^2}\]
Substitute the value of\[\pi = \dfrac{{22}}{7}\]
\[ \Rightarrow \]Area of semicircle AEC \[ = \dfrac{{22}}{{7 \times 2}} \times \dfrac{{35 \times 35}}{{2 \times 2}}\]
Cancel same factors from numerator and denominator
\[ \Rightarrow \]Area of semicircle AEC \[ = \left( {\dfrac{{11 \times 5 \times 35}}{{2 \times 2}}} \right)\]\[c{m^2}\]
\[ \Rightarrow \]Area of semicircle AEC \[ = \left( {\dfrac{{1925}}{4}} \right)\]\[c{m^2}\]
\[ \Rightarrow \]Area of semicircle AEC \[ = 481.25\]\[c{m^2}\]...................… (4)
We know the shaded region is given by subtracting the area of the quadrant from the sum of areas of semicircle and triangle.
Area of shaded area is given by subtracting equation (1) from sum of equations (2) and (4)
\[ \Rightarrow \]Area of shaded region \[ = (481.25 + 294) - (346.5)\]\[c{m^2}\]
\[ \Rightarrow \]Area of shaded region \[ = 428.75\]\[c{m^2}\]
\[\therefore \]Area of shaded region is\[428.75\]\[c{m^2}\]
Now we have to calculate the perimeter of the shaded region.
Perimeter of the shaded region has circumference of the quadrant, circumference of the semicircle and the line AD.
(i) Quadrant:
Circumference of quadrant \[ = \dfrac{{2\pi r}}{4}\]
Here value of \[r = 21\]as \[BC = 21\]cm
\[ \Rightarrow \]Circumference of quadrant \[ = \left( {2 \times \dfrac{{22}}{7} \times \dfrac{{21}}{4}} \right)\]cm
Cancel same factors from numerator and denominator
\[ \Rightarrow \]Circumference of quadrant \[ = \left( {11 \times 3} \right)\]cm
\[ \Rightarrow \]Circumference of quadrant \[ = 33\]cm………………….… (5)
(ii) Semicircle:
Circumference of semicircle \[ = \dfrac{{2\pi r}}{2}\]
\[ \Rightarrow \]Circumference of semicircle \[ = \pi r\]
Here value of \[r = \dfrac{{35}}{2}\]as \[AC = 35\]cm is the diameter of the semicircle
\[ \Rightarrow \]Circumference of semicircle \[ = \left( {\dfrac{{22}}{7} \times \dfrac{{35}}{2}} \right)\]cm
Cancel same factors from numerator and denominator
\[ \Rightarrow \]Circumference of semicircle \[ = \left( {11 \times 5} \right)\]cm
\[ \Rightarrow \]Circumference of semicircle \[ = 55\]cm……………….… (6)
(iii) AD:
We know \[AD = AB - BD\]
Substitute the value of \[AB = 28;BD = 21\]
\[ \Rightarrow AD = \left( {28 - 21} \right)\]cm
\[ \Rightarrow AD = 7\]cm…………...… (7)
So, the perimeter of the shaded area is sum of equations (5), (6) and (7)
\[ \Rightarrow \]Perimeter \[ = (33 + 55 + 7)\]cm
\[ \Rightarrow \]Perimeter \[ = 95\]cm
\[\therefore \]Perimeter of the shaded region is 95cm.
Note: Students are likely to make the mistake of calculating the perimeter wrong as they add the complete perimeter of the quadrant and the semicircle and add them. Keep in mind the radius of both semicircles and the quadrant plays no role in the perimeter of the shaded area. Perimeter is the boundary of the shaded region and that is made up of the part of circumferences of the quadrant and semicircle.
Recently Updated Pages
Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Trending doubts
Which places in India experience sunrise first and class 9 social science CBSE

Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Write the 6 fundamental rights of India and explain in detail

Difference Between Plant Cell and Animal Cell

What is the Full Form of ISI and RAW

Golden Revolution is related to AFood production BOil class 9 social science CBSE




