Question

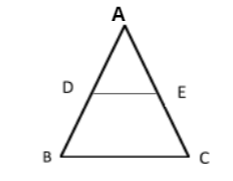
In the given figure, \[DE\parallel BC\], AD = 2 cm, DB = 3cm and AE = 1.6 cm. Then EC is equal to
A) 1.2cm
B) 2.5cm
C) 2.4cm
D) 4.8cm

Answer 1

Hint: In this question we will simply use the basic proportionality theorem of triangles to find out EC.
As there is a triangle given to us and \[DE\parallel BC\]
By using the theorem we will find out ratios to sides and thus we will find EC.

Complete step-by-step answer:
In triangle ABC,
D is point on AB and E is point on AC and \[DE\parallel BC\]
Basic Proportionality theorem states that if a line is drawn parallel to the one side of the to intersect the other two sides in distinct points, the other two sides are divided in the same ratio,
which implies \[\dfrac{{AD}}{{DB}} = \dfrac{{AE}}{{EC}}\]……………………… (1)
putting the values of AD, DB, AE, taking EC as EC
we have
$\Rightarrow$$\dfrac{2}{3}\, = \,\dfrac{{1.6}}{{EC}}$ …………………………….(2)
Solving this above ratio found in (2)
$\Rightarrow$$EC$ = $\dfrac{{1.6\, \times \,3}}{2}$ cm
$\Rightarrow$$EC$ = $(0.8 \times 3 )$ cm
$\Rightarrow$$EC = 2.4 cm$
Therefore length of EC = 2.4 cm

Hence option (c) is the correct option.

Note: In case you did not remember basic proportionality theorem you can go for solving the question just by making ratios with respect to sides. Another method is using algebraic operations and using algebraic methods lots of complication will be there and it can also cause lots of error so it is always better either keep theorem in your mind or use the trick .
Trick whatsoever points are given on sides, go for creating ratio for them and then solve for unknown values. As D was pointed to AB , therefore the ratio came out to be AD/DB.