
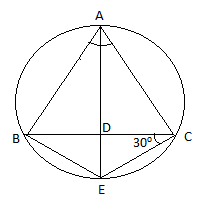
In the given figure, \[\Delta ABC\] is inscribed in a circle. The bisector of \[\angle BAC\] meets BC at D and the circle at E. If EC is joined then \[\angle ECD={{30}^{\circ }}\]. The value of \[\angle BAC\] is:
A. \[{{30}^{\circ }}\]
B. \[{{40}^{\circ }}\]
C. \[{{50}^{\circ }}\]
D. \[{{60}^{\circ }}\]\[\]

Answer
603.9k+ views
Hint: The angles, subtended by a chord of a circle to the circumference of the same circle, are equal. Thus angle A is bisected so \[\angle BAE\] is equal to \[\angle EAC\]. Thus find \[\angle BAC\].
Complete step-by-step answer:
We have been given a triangle ABC which is inscribed in a circle.AE is the bisector of \[\angle BAC\] and it meets BC at D and the arc BEC at E.
We have been given \[\angle ECD={{30}^{\circ }}\], by joining EC.
Let us join BE.
Now BE is the chord of the given circle.
The angle subtended by a chord in a circle, to the circumference of the same circle at different points are equal.
Thus the chord of the given circle subtends equal angles at \[\angle BAE\] and \[\angle BCE\].
Thus we can say that,
\[\angle BAE=\angle BCE\].
We have been told that AE is the bisector of angle A.
A bisector divides the angle into 2 equal halves.
\[\therefore \angle BAE=\angle EAC\]
Thus we got that \[\angle BAE=\angle BCE\] and \[\angle BAE=\angle EAC\].
Thus we can say that \[\angle BCE=\angle EAC\].
We know the value of \[\angle BCE={{30}^{\circ }}\].
\[\therefore \angle BCE=\angle EAC={{30}^{\circ }}\].
We need to find \[\angle BAC\]. AE is a bisector, so
\[\angle A=\angle BAE+\angle EAC\].
We have got \[\angle BAE={{30}^{\circ }}\] and \[\angle EAC={{30}^{\circ }}\].
\[\therefore \angle A=\angle BAE+\angle EAC={{30}^{\circ }}+{{30}^{\circ }}={{60}^{\circ }}\].
Thus we got \[\angle BAC={{60}^{\circ }}\].
Option D is the correct answer.
Note: We can only solve this problem by using the theorem of the angle subtended by a chord. You should also remember that an angle bisector divides the angle into 2 equal halves.
Complete step-by-step answer:
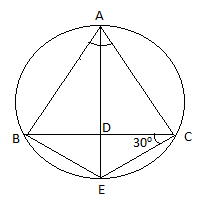
We have been given a triangle ABC which is inscribed in a circle.AE is the bisector of \[\angle BAC\] and it meets BC at D and the arc BEC at E.

We have been given \[\angle ECD={{30}^{\circ }}\], by joining EC.
Let us join BE.
Now BE is the chord of the given circle.
The angle subtended by a chord in a circle, to the circumference of the same circle at different points are equal.
Thus the chord of the given circle subtends equal angles at \[\angle BAE\] and \[\angle BCE\].
Thus we can say that,
\[\angle BAE=\angle BCE\].
We have been told that AE is the bisector of angle A.
A bisector divides the angle into 2 equal halves.
\[\therefore \angle BAE=\angle EAC\]
Thus we got that \[\angle BAE=\angle BCE\] and \[\angle BAE=\angle EAC\].
Thus we can say that \[\angle BCE=\angle EAC\].
We know the value of \[\angle BCE={{30}^{\circ }}\].
\[\therefore \angle BCE=\angle EAC={{30}^{\circ }}\].
We need to find \[\angle BAC\]. AE is a bisector, so
\[\angle A=\angle BAE+\angle EAC\].
We have got \[\angle BAE={{30}^{\circ }}\] and \[\angle EAC={{30}^{\circ }}\].
\[\therefore \angle A=\angle BAE+\angle EAC={{30}^{\circ }}+{{30}^{\circ }}={{60}^{\circ }}\].
Thus we got \[\angle BAC={{60}^{\circ }}\].
Option D is the correct answer.
Note: We can only solve this problem by using the theorem of the angle subtended by a chord. You should also remember that an angle bisector divides the angle into 2 equal halves.
Recently Updated Pages
Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Trending doubts
The shortest day of the year in India

Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

What is the median of the first 10 natural numbers class 10 maths CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

State and prove converse of BPT Basic Proportionality class 10 maths CBSE




