Question

In the given figure, \[\Delta ABC\] is an equilateral triangle of side 3 units. Find the coordinates of the other two vertices.

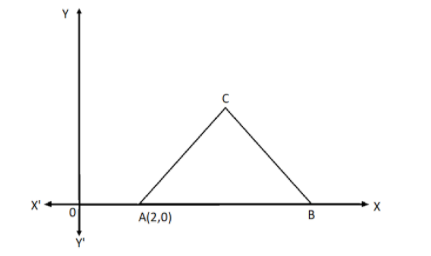
Answer 1

Hint: Here we will first find the coordinates of the point B as it lies on the X-axis. Then we will find the equation of the side using the formula of the distance between the two points. We will then equate the two side’s equations to get the value of the coordinates of the point C.

Formula used:
 The distance between the two points with coordinates \[\left( {{x_1},{y_1}} \right),\left( {{x_2},{y_2}} \right)\] is given by\[d = \sqrt {{{({x_2} - {x_1})}^2} + {{({y_2} - {y_1})}^2}} \].

Complete step-by-step answer:
It is given that the side of the equilateral triangle is equal to 3 units. Therefore, we get
\[AB = BC = AC = 3\]
Let the coordinates of the point B be \[\left( {{x_2},0} \right)\]. The Y coordinate of the point B is zero as the point lies on the X-axis.
Let the coordinates of the point C be \[\left( {{x_3},{y_3}} \right)\].
We know that the coordinates of a point is the distance of that point from the origin O on the respective axis.
From the figure, the point B is lying on the X-axis. So the X coordinate of the point B is
\[{x_2} = 2 + AC\]
Substituting \[AC = 3\] in the above equation, we get
\[{x_2} = 2 + 3 = 5\]
Hence the coordinates of the point B is \[\left( {5,0} \right)\].
Now we will find the coordinates of the point C.
It is given that \[AC = 3\].
Now by using the formula for the distance between the two points we get the value of AC as
\[AC = \sqrt {{{\left( {{x_3} - 2} \right)}^2} + {{\left( {{y_3} - 0} \right)}^2}} = 3\]
Now squaring both side of the equation we get
\[ \Rightarrow A{C^2} = {\left( {{x_3} - 2} \right)^2} + {\left( {{y_3} - 0} \right)^2} = 9\]
\[ \Rightarrow A{C^2} = {\left( {{x_3} - 2} \right)^2} + {y_3}^2 = 9\]………………………\[\left( 1 \right)\]
Similarly now we will find for side BC, we get
\[ \Rightarrow B{C^2} = {\left( {{x_3} - 5} \right)^2} + {\left( {{y_3} - 0} \right)^2} = 9\]
\[ \Rightarrow B{C^2} = {\left( {{x_3} - 5} \right)^2} + {y_3}^2 = 9\]………………………\[\left( 2 \right)\]
Now from the equation \[\left( 1 \right)\] and equation \[\left( 2 \right)\], we get
\[{\left( {{x_3} - 2} \right)^2} + {y_3}^2 = {\left( {{x_3} - 5} \right)^2} + {y_3}^2\]
\[ \Rightarrow {\left( {{x_3} - 2} \right)^2} = {\left( {{x_3} - 5} \right)^2}\]
Now by solving this we will get the value of the \[{x_3}\], we get
\[ \Rightarrow {x_3}^2 + 4 - 4{x_3} = {x_3}^2 + 25 - 10{x_3}\]
Simplifying the equation, we get
\[ \Rightarrow 10{x_3} - 4{x_3} = 25 - 4\]
Subtracting the terms, we get
\[ \Rightarrow 6{x_3} = 21\]
Now dividing both sides by 6, we get
\[ \Rightarrow {x_3} = \dfrac{{21}}{6} = \dfrac{7}{2}\]
Now we will put the value of \[{x_3}\] in the equation \[\left( 1 \right)\] to get the value of \[{y_3}\]. Therefore, we get
\[A{C^2} = {\left( {\dfrac{7}{2} - 2} \right)^2} + {y_3}^2 = 9\]
\[ \Rightarrow {\left( {\dfrac{{7 - 4}}{2}} \right)^2} + {y_3}^2 = 9\]
Now by solving this above equation, we get
\[ \Rightarrow {\left( {\dfrac{3}{2}} \right)^2} + {y_3}^2 = 9\]
Applying the exponent on the terms, we get
\[ \Rightarrow \dfrac{9}{4} + {y_3}^2 = 9\]
\[ \Rightarrow {y_3}^2 = 9 - \dfrac{9}{4}\]
Taking LCM on RHS, we get
\[ \Rightarrow {y_3}^2 = \dfrac{{36 - 9}}{4} = \dfrac{{27}}{4}\]
Taking square root on both sides, we get
\[ \Rightarrow {y_3} = \dfrac{{3\sqrt 3 }}{2}\]
Therefore the coordinates of the point C is \[\left( {\dfrac{7}{2},\dfrac{{3\sqrt 3 }}{2}} \right)\].
Hence the coordinates of the point B is \[\left( {5,0} \right)\] and coordinates of point C is \[\left( {\dfrac{7}{2},\dfrac{{3\sqrt 3 }}{2}} \right)\].

Note: We should note that while writing the coordinates of a point always the X-axis intercept of the point is written first and then the Y-axis intercept is written. Also, the positive X-axis is towards the right side of the origin and negative X-axis is towards the left side of the origin. The positive Y-axis is towards the upward direction from the origin and negative Y-axis is towards the downward direction from the origin.
Points which lie on the X-axis have the Y coordinate equal to zero and the points lying on the Y-axis have the X coordinate equal to zero.