Question

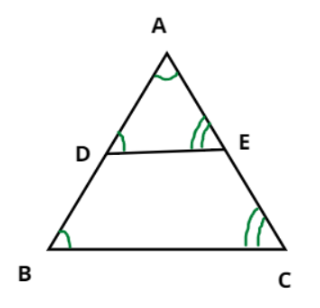
In the given figure, DE is parallel to BC
\[{\text{(i)}}\] If \[{\text{DE = 4 cm, BC = 6 cm}}\] and \[{\text{Area(}}\vartriangle {\text{ADE) = 16 c}}{{\text{m}}^{\text{2}}}\], find the area of \[\vartriangle {\text{ABC}}\].
\[{\text{(ii)}}\] If \[{\text{DE = 4 cm, BC = 8 cm}}\] and \[{\text{Area(}}\vartriangle {\text{ADE) = 25 c}}{{\text{m}}^{\text{2}}}\], find the area of \[\vartriangle {\text{ABC}}\].
\[{\text{(iii)}}\] If \[{\text{DE:BC = 3:5}}\]. Calculate the ratio of the areas of \[\vartriangle {\text{ADE}}\] and the area of BCED.

Answer 1

Hint- Here, we will be using the properties of congruent triangles.
Given, DE is parallel to BC.
From the figure, in \[\vartriangle {\text{ADE}}\] and \[\vartriangle {\text{ABC}}\]
\[\angle {\text{A = }}\angle {\text{A}}\] (Common angle)
Since, DE is parallel to BC therefore the below angles will be equal because they are corresponding angles.
\[ \Rightarrow \angle {\text{D = }}\angle {\text{B}}\] (Corresponding angles) and (Corresponding angles)
Therefore, by AAA congruence criteria, the triangles ADE and ABC are congruent
i.e., \[\vartriangle {\text{ADE}} \cong \vartriangle {\text{ABC}}\]
\[{\text{(i)}}\] Given, \[{\text{DE = 4 cm, BC = 6 cm}}\] and \[{\text{Area(}}\vartriangle {\text{ADE) = 16 c}}{{\text{m}}^{\text{2}}}\]
Since, for two congruent triangles, the ratio of their areas will be equal to the square of the ratio of their corresponding sides.
As, \[\vartriangle {\text{ADE}} \cong \vartriangle {\text{ABC}} \Rightarrow \dfrac{{{\text{Area(}}\vartriangle {\text{ADE)}}}}{{{\text{Area(}}\vartriangle {\text{ABC)}}}} = {\left( {\dfrac{{{\text{DE}}}}{{{\text{BC}}}}} \right)^2} \Rightarrow \dfrac{{16}}{{{\text{Area(}}\vartriangle {\text{ABC)}}}} = {\left( {\dfrac{{\text{4}}}{{\text{6}}}} \right)^2} = \dfrac{{16}}{{36}}\]
\[ \Rightarrow {\text{Area(}}\vartriangle {\text{ABC)}} = \dfrac{{36 \times 16}}{{16}} = 36{\text{ c}}{{\text{m}}^2}\]
Therefore, the area of triangle ABC is \[36{\text{ c}}{{\text{m}}^2}\].
\[{\text{(ii)}}\] Given, \[{\text{DE = 4 cm, BC = 8 cm}}\] and \[{\text{Area(}}\vartriangle {\text{ADE) = 25 c}}{{\text{m}}^{\text{2}}}\]
Since, for two congruent triangles, the ratio of their areas will be equal to the square of the ratio of their corresponding sides.
As, \[\vartriangle {\text{ADE}} \cong \vartriangle {\text{ABC}} \Rightarrow \dfrac{{{\text{Area(}}\vartriangle {\text{ADE)}}}}{{{\text{Area(}}\vartriangle {\text{ABC)}}}} = {\left( {\dfrac{{{\text{DE}}}}{{{\text{BC}}}}} \right)^2} \Rightarrow \dfrac{{25}}{{{\text{Area(}}\vartriangle {\text{ABC)}}}} = {\left( {\dfrac{{\text{4}}}{8}} \right)^2} = \dfrac{{16}}{{64}}\]
\[ \Rightarrow {\text{Area(}}\vartriangle {\text{ABC)}} = \dfrac{{25 \times 64}}{{16}} = 100{\text{ c}}{{\text{m}}^2}\]
Therefore, the area of triangle ABC is \[{\text{100 c}}{{\text{m}}^2}\].
\[(iii)\] Given, \[{\text{DE:BC = 3:5}} \Rightarrow \dfrac{{{\text{DE}}}}{{{\text{BC}}}} = \dfrac{3}{5}\]
Since, for two congruent triangles, the ratio of their areas will be equal to the square of the ratio of their corresponding sides.
As, \[\vartriangle {\text{ADE}} \cong \vartriangle {\text{ABC}} \Rightarrow \dfrac{{{\text{Area(}}\vartriangle {\text{ADE)}}}}{{{\text{Area(}}\vartriangle {\text{ABC)}}}} = {\left( {\dfrac{{{\text{DE}}}}{{{\text{BC}}}}} \right)^2} = {\left( {\dfrac{3}{5}} \right)^2} = \dfrac{9}{{25}} \Rightarrow \dfrac{{{\text{Area(}}\vartriangle {\text{ADE)}}}}{{{\text{Area(}}\vartriangle {\text{ADE) + Area(BCED)}}}} = \dfrac{9}{{25}}\]
Reciprocating the above equation, we get
\[
   \Rightarrow \dfrac{{{\text{Area(}}\vartriangle {\text{ADE) + Area(BCED)}}}}{{{\text{Area(}}\vartriangle {\text{ADE)}}}} = \dfrac{{25}}{9} \Rightarrow \dfrac{{{\text{Area(}}\vartriangle {\text{ADE)}}}}{{{\text{Area(}}\vartriangle {\text{ADE)}}}} + \dfrac{{{\text{Area(BCED)}}}}{{{\text{Area(}}\vartriangle {\text{ADE)}}}} = \dfrac{{25}}{9} \\
   \Rightarrow {\text{1}} + \dfrac{{{\text{Area(BCED)}}}}{{{\text{Area(}}\vartriangle {\text{ADE)}}}} = \dfrac{{25}}{9} \Rightarrow \dfrac{{{\text{Area(BCED)}}}}{{{\text{Area(}}\vartriangle {\text{ADE)}}}} = \dfrac{{25}}{9} - 1 = \dfrac{{16}}{9} \\
 \]
Now again reciprocating the above equation, we get
\[ \Rightarrow \dfrac{{{\text{Area(}}\vartriangle {\text{ADE)}}}}{{{\text{Area(BCED)}}}} = \dfrac{9}{{16}}\]
Therefore, the ratio of triangle ADE to the quadrilateral BCED is \[{\text{9:16}}\].

Note- These type of problems are mostly solved with the help of geometry. Hence, congruency rule is used to obtain the relation between known and unknown data. By these relations, the required value of the unknown can be computed easily.