Question

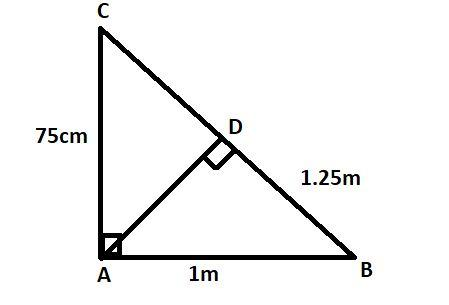
In the given figure \[\angle CAB{\text{ = 9}}{{\text{0}}^0}\]and\[AD \bot BC\]. If\[AC = 75{\text{ }}cm\], \[AB = 1m\]and\[BD = 1.25m\], find \[AD\]

Answer 1

 Hint:-Here, we go through the property of a similar triangle to find the unknown value.

We have
$AB = 1{\text{ }}m = 100{\text{ }}cm,{\text{ }}AC = 75{\text{ }}cm$ and $BD = 125{\text{ }} cm$.

In $\vartriangle BAC$ and$\vartriangle BDA$, we have
$\angle BAC = \angle BDA\;{\text{ }}\;{\text{ }}$ [Each angle equal to${90^0}$]
And $\angle ABD = \angle ABC$

So, by AA - criterion of similarity, we have
$\vartriangle BAC \sim \vartriangle BDA$

By the property of similar triangle
$ \Rightarrow \dfrac{{BA}}{{BD}} = \dfrac{{AC}}{{AD}}$ $\because $ Given that $BA = 100cm,BD = 125cm,AC = 75cm$
$ \Rightarrow AD = \dfrac{{125 \times 75}}{{100}} cm = 93.75 cm$

Note: - Whenever we face such a type of question we have to recall the property of a similar triangle. We have to show the similar relation between the triangles and then apply their property to solve the question.