Question

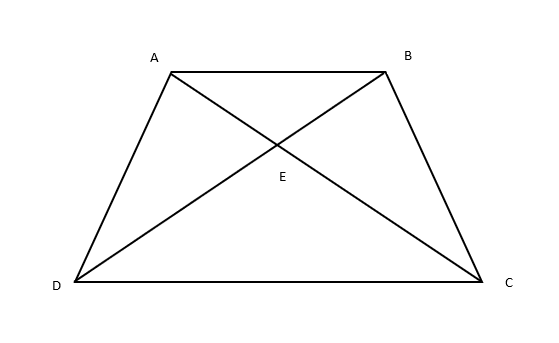
In the given figure, ABCD is a trapezium with ${\text{AB}}\ parallel {\text{DC}}$. If $\Delta AED$ is similar to $\Delta BEC$. Prove that AD = BC

Answer 1

Hint- Check for the relation between corresponding angles and sides of both triangles.

Given: \[ABCD\] is a trapezium with ${\text{AB}}\parallel {\text{DC}}$.
Diagonals $AC$ and $BD$ intersect at point $E$.
To prove: ${\text{AD = BC}}$
Now, $\Delta AED \sim \Delta BEC{\text{ }}\left( {\because {\text{Given}}} \right)$
$\therefore \dfrac{{{\text{AE}}}}{{{\text{BE}}}}{\text{ = }}\dfrac{{{\text{ED}}}}{{{\text{EC}}}}{\text{ = }}\dfrac{{{\text{AD}}}}{{{\text{BC}}}}{\text{ }} \ldots \ldots \left( 1 \right)\left( {{\text{corresponding sides are proportional}}} \right)$
In \[\Delta {\text{ABE}}\]and \[\Delta {\text{CDE}}\]:
\[
  \angle {\text{AEB = }}\angle {\text{CED }}\left( {{\text{vertically opposite angles}}} \right) \\
  \angle {\text{EAB}} = {\text{ }}\angle {\text{ECD }}\left( {{\text{alternate angles}}} \right) \\
\]
Hence, by AA similarity, we can say
\[\Delta {\text{ABE}} \sim \Delta {\text{CDE }}\]
Now, \[\dfrac{{{\text{AB}}}}{{{\text{CD}}}} = \dfrac{{{\text{EB}}}}{{{\text{ED}}}} = \dfrac{{{\text{AE}}}}{{{\text{EC}}}}{\text{ }}\left( {\because {\text{corresponding sides are proportional}}} \right)\]
Therefore, \[\dfrac{{{\text{EC}}}}{{{\text{ED}}}} = \dfrac{{{\text{AE}}}}{{{\text{EB}}}}{\text{ }} \ldots \ldots \left( 2 \right)\]
From \[\left( 1 \right)\]and \[\left( 2 \right)\], we get
\[\dfrac{{{\text{AD}}}}{{{\text{BC}}}} = \dfrac{{{\text{ED}}}}{{{\text{EC}}}}\]
As we know, \[{\text{ED = EC}}\]
\[
   \Rightarrow \dfrac{{{\text{AD}}}}{{{\text{BC}}}} = 1{\text{ }} \\
  \therefore {\text{ AD = BC}} \\
\]
Hence Proved.

Note- Two triangles are similar if their corresponding angles are congruent and corresponding sides are proportional. There are many criterions of similarity and many properties of similar triangles which come handy while solving problems like these.