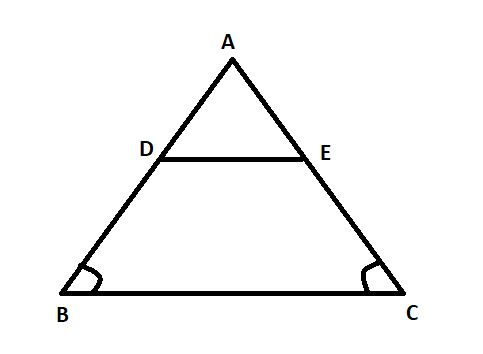
In the given figure ${\text{ABC}}$ is a triangle in which ${\text{AB = AC}}$. Points ${\text{D}}$ and ${\text{E}}$ are points on the sides ${\text{AB}}$and ${\text{AC}}$ respectively such that ${\text{AD = AE}}$. Show that the points ${\text{B,C,E}}$and ${\text{D}}$ are concyclic.
Answer
Verified363.9k+ views
Hint: - Here, we go with the property of parallel lines and with the property of cyclic quadrilaterals. In a cyclic quadrilateral, the sum of either pair of opposite angles is supplementary.
In order to prove that the points ${\text{B,C,E}}$and ${\text{D}}$ are concyclic, it is sufficient to show that \[\angle ABC + \angle CED = {180^0}\] and \[\angle ACB + \angle BDE = {180^0}\].
In\[\;\vartriangle ABC\], we have
\[AB = AC\]And \[AD = AE\]
\[
\Rightarrow \;AB - AD = AC - AE \\
\Rightarrow \;DB = EC \\
\]
Thus, we have
\[AD = AE\;\]And \[DB = EC\;\]
\[ \Rightarrow \frac{{AD}}{{DB}} = \frac{{AE}}{{EC}}\]
\[ \Rightarrow \;{\text{ }}\;DE\mid \mid BC\;{\text{ }}\] [By the converse of Thales Theorem]
\[ \Rightarrow \;{\text{ }}\;\angle ABC = \angle ADE\;{\text{ }}\;{\text{ }}\] [Corresponding angles]
\[ \Rightarrow \;{\text{ }}\;\angle ABC + \angle BDE = \angle ADE + \angle BDE\] [Adding \[\angle BDE\]both sides]
\[ \Rightarrow \;\;\angle ABC + \angle BDE = {180^0}{\text{ }}\] \[\because \angle BDE + \angle ADE = {180^0}\](Straight angle)
\[ \Rightarrow \;{\text{ }}\;\angle ACB + \angle BDE = {180^0}\] [\[\because AB = AC\]And\[\therefore \angle ABC = \angle ACB\]]
Again, \[DE\mid \mid BC\]
\[ \Rightarrow \;{\text{ }}\;\;\angle ACB = \angle AED\]
\[ \Rightarrow \;{\text{ }}\;\angle ACB + \angle CED = \angle AED + \angle CED\;\] [Adding \[\angle CED\]both sides]
\[ \Rightarrow \;\;\angle ACB + \angle CED = {180^0}\] \[\because \angle AED + \angle CED = {180^0}\](Straight angle)
\[ \Rightarrow \;\;\angle ABC + \angle CED = {180^0}\] [\[\because \angle ABC = \angle ACB\]]
Thus, \[BDEC\] is a cyclic quadrilateral because the sum of alternate angles are supplementary Hence ${\text{B,C,E}}$and ${\text{D}}$ are concyclic points.
Note:-This question is based on the property of parallel lines and their corresponding angles and also on the property of the isosceles triangle. By applying these properties we can easily solve such types of questions for showing cyclic quadrilaterals
In order to prove that the points ${\text{B,C,E}}$and ${\text{D}}$ are concyclic, it is sufficient to show that \[\angle ABC + \angle CED = {180^0}\] and \[\angle ACB + \angle BDE = {180^0}\].
In\[\;\vartriangle ABC\], we have
\[AB = AC\]And \[AD = AE\]
\[
\Rightarrow \;AB - AD = AC - AE \\
\Rightarrow \;DB = EC \\
\]
Thus, we have
\[AD = AE\;\]And \[DB = EC\;\]
\[ \Rightarrow \frac{{AD}}{{DB}} = \frac{{AE}}{{EC}}\]
\[ \Rightarrow \;{\text{ }}\;DE\mid \mid BC\;{\text{ }}\] [By the converse of Thales Theorem]
\[ \Rightarrow \;{\text{ }}\;\angle ABC = \angle ADE\;{\text{ }}\;{\text{ }}\] [Corresponding angles]
\[ \Rightarrow \;{\text{ }}\;\angle ABC + \angle BDE = \angle ADE + \angle BDE\] [Adding \[\angle BDE\]both sides]
\[ \Rightarrow \;\;\angle ABC + \angle BDE = {180^0}{\text{ }}\] \[\because \angle BDE + \angle ADE = {180^0}\](Straight angle)
\[ \Rightarrow \;{\text{ }}\;\angle ACB + \angle BDE = {180^0}\] [\[\because AB = AC\]And\[\therefore \angle ABC = \angle ACB\]]
Again, \[DE\mid \mid BC\]
\[ \Rightarrow \;{\text{ }}\;\;\angle ACB = \angle AED\]
\[ \Rightarrow \;{\text{ }}\;\angle ACB + \angle CED = \angle AED + \angle CED\;\] [Adding \[\angle CED\]both sides]
\[ \Rightarrow \;\;\angle ACB + \angle CED = {180^0}\] \[\because \angle AED + \angle CED = {180^0}\](Straight angle)
\[ \Rightarrow \;\;\angle ABC + \angle CED = {180^0}\] [\[\because \angle ABC = \angle ACB\]]
Thus, \[BDEC\] is a cyclic quadrilateral because the sum of alternate angles are supplementary Hence ${\text{B,C,E}}$and ${\text{D}}$ are concyclic points.
Note:-This question is based on the property of parallel lines and their corresponding angles and also on the property of the isosceles triangle. By applying these properties we can easily solve such types of questions for showing cyclic quadrilaterals
Last updated date: 22nd Sep 2023
•
Total views: 363.9k
•
Views today: 6.63k
