Question

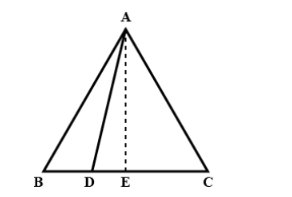
In the given figure ABC is a triangle in which AB=AC and D is any point in BC. Prove that $$A{B^2} - A{D^2} = BD.CD$$

Answer 1

Hint: We need to draw a perpendicular from A to BC which divides the triangle into two equal parts.
Draw $AE \bot BC$
In $\Delta AEB$ and $\Delta AEC$, we have
From the given information $AB = AC$
$AE = AE$ [Common to both triangles AEB and AEC] and
$\angle b = \angle c$ [Because AB=AC]
$\therefore \Delta AEB \cong \Delta AEC$
$ \Rightarrow BE = CE$
Since $\Delta AED$ and $\Delta ABE$ are right angles triangles at E.
Therefore, Using Pythagoras theorem we can write
$A{D^2} = A{E^2} + D{E^2}$-- (1)
$A{B^2} = A{E^2} + B{E^2}$--- (2)
Subtracting the (2) – (1)
$ \Rightarrow A{B^2} - A{D^2} = B{E^2} - D{E^2}$
$ \Rightarrow A{B^2} - A{D^2} = \left( {BE + DE} \right)\left( {BE - DE} \right)$ $\left[ {\because {a^2} - {b^2} = (a + b)(a - b)} \right]$
$ \Rightarrow A{B^2} - A{D^2} = \left( {CE + DE} \right)\left( {BE - DE} \right)$ $\left[ {\because BE = CE} \right]$
By observing the figure we can easily understand that CE + DE = CD and BE – DE = BD
$ \Rightarrow A{B^2} - A{D^2} = CD \cdot BD$
$ \Rightarrow A{B^2} - A{D^2} = BD \cdot CD$
Hence proved

Note: We have drawn a perpendicular from A to BC to make the resulting triangles congruent. When two triangles are congruent they will have exactly the same three sides and exactly the same three angles.