Question

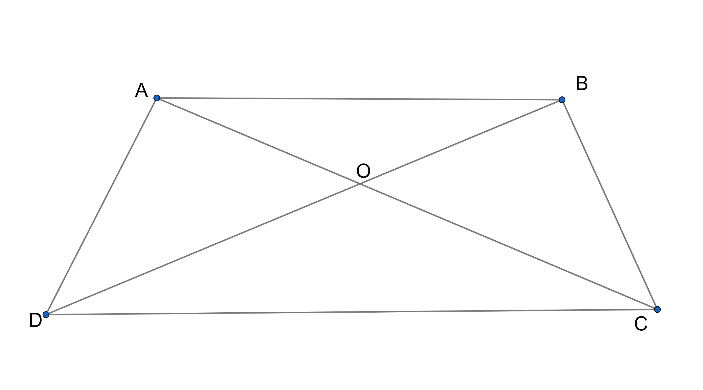
In the given figure $ABC$ and $DBC$ are two triangles on the same base. if $AD$ intersects $BC$ at $O$, show that:
$\dfrac{area(\Delta ABC)}{area(\Delta DBC)}=\dfrac{AO}{DO}$

Answer 1

Hint: Draw $AE$ perpendicular to$BC$ and $DF$perpendicular to$BC$and prove the triangles equal and find the area. For calculation of area of a triangle use
Area of Triangle$=\dfrac{1}{2}\times $base$\times $ height

Complete step by step answer:
It is given that $\Delta ABC$ and $\Delta DBC$ have the same base $BC$ .
We want to prove that $\dfrac{area(\Delta ABC)}{area(\Delta DBC)}=\dfrac{AO}{DO}$ .
So here we can see that $AO$ and $DO$ are part of $\Delta ABC$ and $\Delta DBC$ ,
We know that,
Area of Triangle$=\dfrac{1}{2}\times $ base $\times $ height
Now draw altitude $AE$ perpendicular to $BC$ and $DF$ perpendicular to $BC$ , So such that we can relate a part.
So the figure becomes as follows,

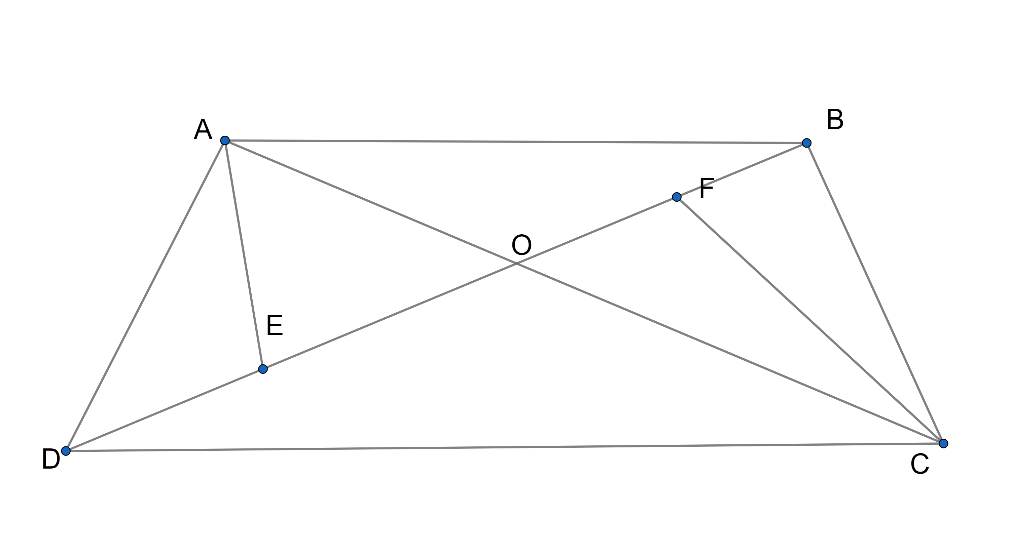
Now in $\Delta ABC$ and $\Delta DBC$ , We get area as follows,
$area\Delta ABC=\dfrac{1}{2}\times BC\times AE$ and $area\Delta DBC=\dfrac{1}{2}\times BC\times DF$
Now taking ratio of area of $\Delta ABC$ to area of $\Delta DBC$ We get,
So the ratio is as follows,
$\begin{align}
  & \dfrac{area(\Delta ABC)}{area(\Delta DBC)}=\dfrac{\dfrac{1}{2}\times BC\times AE}{\dfrac{1}{2}\times BC\times DF} \\
 & \\
\end{align}$
$\dfrac{area(\Delta ABC)}{area(\Delta DBC)}=\dfrac{AE}{DF}$ ……….. (1)
But in question it is given to prove that ,
$\dfrac{area(\Delta ABC)}{area(\Delta DBC)}=\dfrac{AO}{DO}$
So for this we need to prove that ,
$\dfrac{AE}{DF}=\dfrac{AO}{DO}$
So we need to prove to get above,
So now considering $\Delta AOE$ and $\Delta DOF$ ,
$\angle AEO=\angle DFO={{90}^{\circ }}$
\[\angle AOE=\angle DOF\] ……………….. (These are vertically opposite angles)
So, AA Similarity is as follows,
The AA similarity postulate and theorem makes it even easier to prove that two triangles are similar. In the interest of simplicity, we'll refer to it as the AA similarity postulate. The AA criterion for triangle similarity states that if two triangles have two pairs of congruent angles, then the triangles are similar.
The postulate states that two triangles are similar if they have two corresponding angles that are congruent or equal in measure.
So by AA Similarity , We get to know that
$\Delta AOE\sim \Delta DOF$
We know that if the two triangles are similar then their corresponding sides are in the same ratio.
So here corresponding sides are in same ratio, so we get,
 $\dfrac{AE}{DF}=\dfrac{AO}{DO}$ ……………. (2)
So from (1) and (2) we get that
$\dfrac{area(\Delta ABC)}{area(\Delta DBC)}=\dfrac{AO}{DO}=\dfrac{AE}{DF}$

So we get the final proved answer,
 $\dfrac{area(\Delta ABC)}{area(\Delta DBC)}=\dfrac{AO}{DO}$
Hence proved.

Note: Here you should know that I have made a construction so you should be knowing how and when to make construction. I got it when I didn’t see any link between $AO$ and $DO$ which were not a part of $\Delta ABC$ and $\Delta DBC$ . So I made a construction in this way. So when I came at $\dfrac{area(ABC)}{area(DBC)}=\dfrac{AE}{DF}$ I got to know that we should prove this $\dfrac{AE}{DF}=\dfrac{AO}{DO}$ to get the answer.