Question

In the following figure, the inscribed circle of $\Delta ABC$ with center P touches the sides AB, BC and AC at points L, M, N respectively. Show that area ($\Delta ABC$) = $\dfrac{1}{2}\times $ (perimeter of $\Delta ABC$) $\times $ (radius of inscribed circle).

Answer 1

Hint: Assume a variable r which will represent the radius of the circle. Find the area of the triangle using the formula $\dfrac{1}{2}\times $ base$\times $ height. The perimeter of the triangle is given by adding the lengths of all the sides of the triangle.

Complete step-by-step answer:
Before proceeding with the question, we must know all the concepts and the formulas that will be required to solve this question.
The area of a triangle is given by the formula,
Area = $\dfrac{1}{2}\times $ base$\times $ height . . . . . . . . . . . . . (1)

If we draw a line from the center of a circle to its point of contact with tangent, then this line is perpendicular to the tangent . . . . . . . . . . (2)

In this question, we are given an inscribed circle of $\Delta ABC$ with center P touching the sides AB, BC and AC at points L, M, N respectively. We are required to show that area ($\Delta ABC$) = $\dfrac{1}{2}\times $ (perimeter of $\Delta ABC$) $\times $ (radius of inscribed circle).

Let us assume that r is that radius of the inscribed circle. So, PL = PM = PN = r.

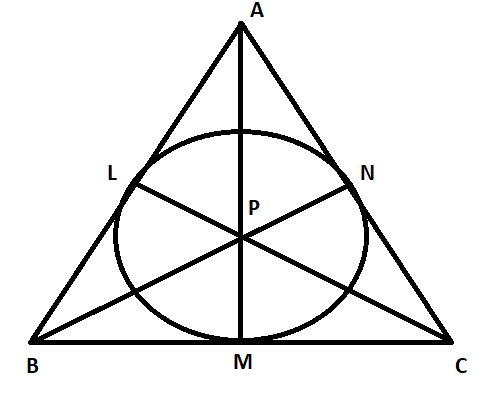
Let us find the area of $\Delta ABC$. It can be observed from the figure that,
Area ($\Delta ABC$) = Area ($\Delta APB$) + Area ($\Delta BPC$) + Area ($\Delta APC$) . . . . . . . . (3)

In the triangle $\Delta APB$, AB is the base of the triangle. Since AB is the tangent to the circle, using concept (2), we can say that PL is perpendicular to AB. So, PL is the height of the triangle $\Delta APB$. Using formula (1), we get,
Area ($\Delta APB$) = $\dfrac{1}{2}\left( AB \right)\left( PL \right)$
$\Rightarrow $ Area ($\Delta APB$) = $\dfrac{1}{2}\left( AB \right)\left( r \right)$

In the triangle $\Delta BPC$, BC is the base of the triangle. Since BC is the tangent to the circle, using concept (2), we can say that PM is perpendicular to BC. So, PM is the height of the triangle $\Delta BPC$. Using formula (1), we get,
Area ($\Delta BPC$) = $\dfrac{1}{2}\left( BC \right)\left( PM \right)$
$\Rightarrow $ Area ($\Delta BPC$) = $\dfrac{1}{2}\left( BC \right)\left( r \right)$

In the triangle $\Delta APC$, AC is the base of the triangle. Since AC is the tangent to the circle, using concept (2), we can say that PN is perpendicular to AC. So, PN is the height of the triangle $\Delta APC$. Using formula (1), we get,
Area ($\Delta APC$) = $\dfrac{1}{2}\left( AC \right)\left( PN \right)$
$\Rightarrow $ Area ($\Delta APC$) = $\dfrac{1}{2}\left( AC \right)\left( r \right)$
Substituting these areas in equation (3), we get,

Area ($\Delta ABC$) = $\dfrac{1}{2}\left( AB \right)\left( r \right)$ + $\dfrac{1}{2}\left( BC \right)\left( r \right)$ + $\dfrac{1}{2}\left( AC \right)\left( r \right)$
$\Rightarrow $ Area ($\Delta ABC$) = $\dfrac{1}{2}\left( AB+BC+AC \right)\left( r \right)$

The perimeter of the triangle is equal to the sum of lengths of the sides of the triangle. So, the perimeter of $\Delta ABC$ is AB + BC + AC. Also, r is the radius of the inscribed circle. Substituting this in the above equation, we can write,

Area ($\Delta ABC$) = $\dfrac{1}{2}\times $ (perimeter of $\Delta ABC$) $\times $ (radius of inscribed circle).
Hence proved.

Note:
This is an easy question which can be done with the basic knowledge of perimeter and area of the triangle. The only possibility of mistake in this question is the calculation mistake. So in order to avoid this mistake, one must solve this question carefully.