Question

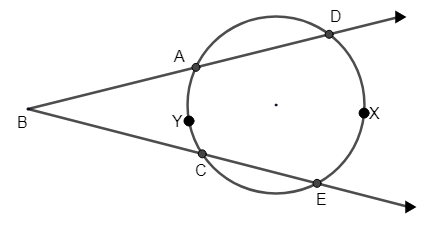
In the following figure, if m (arc DXE) \[={{110}^{\circ }}\] and m (arc AYC) \[={{50}^{\circ }}\]. Find the \[\angle DBE\].
: In the following figure, if m (arc DXE) \[={{110}^{\circ }}\] and m (arc AYC) \[={{50}^{\circ }}\]. Find the \[\angle DBE\].

Answer 1

Hint:Use the inscribed angle theorem and prove that the angle inscribed in the circle is half of the central angle that subtends the same arc on the circle. Join AE and CD, find the angle AEB and DAE using this theorem. By using exterior angle theorem, consider \[\vartriangle AEB\]and find angle ABE.

Complete step-by-step answer:
Given that,
m (arc DXE) \[={{110}^{\circ }}\]
m (arc AYC) \[={{50}^{\circ }}\]
Here, we need to find the angle DBE.

(Figure 1)
Let us use the inscribed angle theorem.
The inscribed angle theorem states that an angle \[\theta \]inscribed in a circle is half of the central angle \[2\theta \]that subtends the same arc on the circle. Therefore the angle does not change if the vertex is moved at different positions on the circle.
Let us consider the center of the circle as O.
According to the theorem, O will not be the point marked, it will be a different point which is the center of the circle, so don’t mark O as the intersection of AE and CD. If possible, draw a line from the center to D and E and mark the center as O too. Angle DOE will be \[2\theta \]only, just the position of O will be different.

(Figure 2)
The angle DOE = \[2\theta \], the angle formed at DAE & DCE is half of angle DOE.
\[\begin{align}
  & \angle DAE=\angle DCE=\dfrac{\angle DOE}{2}=\dfrac{2\theta }{2}=\theta \\
 & \therefore \angle DAE=\angle DCE=\theta \\
\end{align}\]
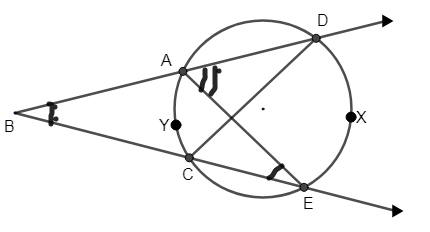
Now let us consider Figure 1, now join AE and CD.
\[\therefore \]Measure of \[\angle AEB=\dfrac{1}{2}\] m (arc AYC)
\[\therefore m\angle AEB=\dfrac{1}{2}\times 50\] i.e. m (arc AYC) \[={{50}^{\circ }}\]
\[m\angle AEB={{25}^{\circ }}\]
Similarly, \[m\angle EAD=\dfrac{1}{2}\] m (arc DXE).
(From the figure), m (arc DXE) \[={{110}^{\circ }}\] from question,
\[\begin{align}
  & m\angle EAD=\dfrac{1}{2}\times {{110}^{\circ }} \\
 & \therefore m\angle EAD={{55}^{\circ }} \\
\end{align}\]
Now let us consider, \[\vartriangle ABE\], where \[\angle DAE\]is an exterior angle.
\[\therefore \]By exterior angle theorem, the measure of an exterior angle is greater than either of the measure of the remote interior angles.

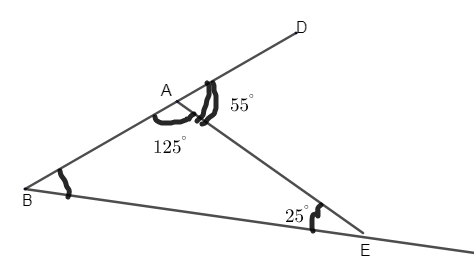
\[\begin{align}
  & \therefore m\angle DAE=m\angle AEB+m\angle ABE \\
 & {{55}^{\circ }}={{25}^{\circ }}+m\angle ABE \\
 & \Rightarrow m\angle ABE={{55}^{\circ }}-{{25}^{\circ }}={{30}^{\circ }} \\
\end{align}\]
Hence, the required angle is \[{{30}^{\circ }}\].
Note:
An inscribed angle can be defined as 2 chords of the circle sharing an end point. The inscribed angle theorem relates the measure of an inscribed angle to that of the central angle subtending the same arc. The exterior angle theorem proves that the sum of the angles of the triangle is \[{{180}^{\circ }}\].
\[\angle BAE={{180}^{\circ }}-{{55}^{\circ }}={{125}^{\circ }}\]
We got, \[\angle ABE={{30}^{\circ }}\].
Sum of angles of \[\vartriangle ABE={{125}^{\circ }}+{{30}^{\circ }}+{{25}^{\circ }}={{180}^{\circ }}\].