Question

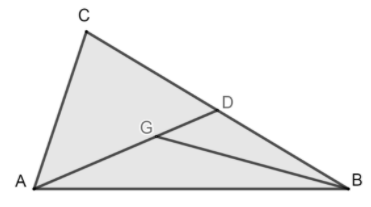
In the following figure, G is the centroid of triangle ABC, show that: $\text{Area}\left( \text{ }\!\!\Delta\!\!\text{ AGB} \right)=\dfrac{2}{3}\times \text{Area}\left( \text{ }\!\!\Delta\!\!\text{ ADB} \right)$ .

Answer 1

Hint: For this question we will proceed by defining the centroid and then eventually define the median of the triangle. We will show it through a figure after that we will write down the properties of the median and then we will take the given figure and then apply the property of median that the three medians divide the triangles into six small triangles of equal area, using this property we will prove the given expression.

Complete step-by-step solution
First, let's understand what a centroid is. So, basically, a centroid is the center point of the object. It is the point at which the three medians of the triangle intersect so a centroid is also defined as the point of intersection of all the three medians. Now we will see what is meant by the median of a triangle. So, a median of a triangle is a line segment that joins a vertex to the midpoint of the side that is opposite to that vertex. Let’s see the following figure:

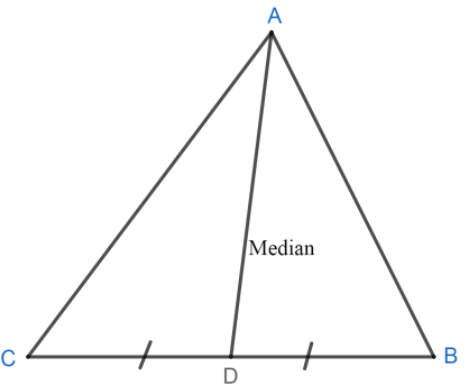
Now in the figure above, AD is the median that divides BC into two equal halves, that is, DB = DC.
Now, we will look at some of the properties of the medians:
A. Every triangle has 3 medians, one from each vertex. AE, BF, and CD are the 3 medians of the triangle ABC is given below.

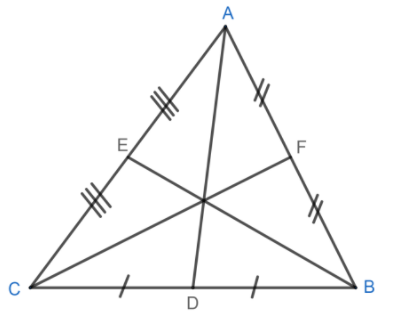
B. Each median of a triangle divides the triangle into two smaller triangles which have equal area and the 3 medians divide the triangle into 6 smaller triangles of equal area.
Now, let’s take the figure given in the question:

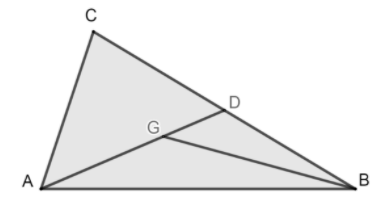
Here, it is given that G is the centroid of triangle ABC, therefore, AD is the median of the given triangle.
Now, we will extend BG to meet the midpoint of AC at E thus giving us our second median BE. Then, we will join the point C and G and extend to meet the midpoint of AB at F thus giving us our last median AF, as shown in the following figure:

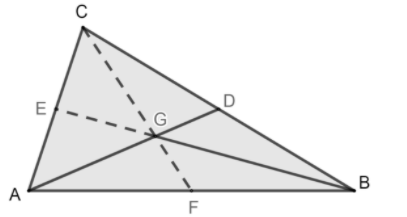
Now, we know that according to the property of medians, all the 3 medians divide the triangle into 6 smaller triangles of equal area. Therefore:
\[\text{Ar}\left( \text{AGF} \right)=\text{Ar}\left( \text{FGB} \right)=\text{Ar}\left( \text{BGD} \right)=\text{Ar}\left( \text{DGC} \right)=\text{Ar}\left( \text{CGE} \right)=\text{Ar}\left( \text{EGA} \right)\text{ }........\left( 1 \right)\]
Now, let’s consider the triangle AGB, now according to the figure we can see that:
$\text{Ar}\left( \text{AGB} \right)=\text{Ar}\left( \text{AGF} \right)+\text{Ar}\left( \text{FGB} \right)$
Now, from equation 1 we know that: $\text{Ar}\left( \text{AGF} \right)=\text{Ar}\left( \text{FGB} \right)$
Therefore,
$\begin{align}
  & \Rightarrow \text{Ar}\left( \text{AGB} \right)=\text{Ar}\left( \text{AGF} \right)+\text{Ar}\left( \text{AGF} \right) \\
 & \Rightarrow \text{Ar}\left( \text{AGB} \right)=2\text{Ar}\left( \text{AGF} \right) \\
 & \Rightarrow \text{Ar}\left( \text{AGF} \right)=\dfrac{\text{Ar}\left( \text{AGB} \right)}{2}\text{ }.......\left( 2 \right) \\
\end{align}$
Now, let’s consider the triangle ADB, now according to the figure we can see that:
$\text{Ar}\left( \text{ADB} \right)=\text{Ar}\left( \text{AGF} \right)+\text{Ar}\left( \text{FGB} \right)+\text{Ar}\left( \text{BGD} \right)$
Now, from equation 1 we know that: $\text{Ar}\left( \text{AGF} \right)=\text{Ar}\left( \text{FGB} \right)=\text{Ar}\left( \text{BGD} \right)$
Therefore:
$\begin{align}
  & \Rightarrow \text{Ar}\left( \text{ADB} \right)=\text{Ar}\left( \text{AGF} \right)+\text{Ar}\left( \text{AGF} \right)+\text{Ar}\left( \text{AGF} \right) \\
 & \Rightarrow \text{Ar}\left( \text{ADB} \right)=3\text{Ar}\left( \text{AGF} \right) \\
 & \Rightarrow \text{Ar}\left( \text{AGF} \right)=\dfrac{\text{Ar}\left( \text{ADB} \right)}{3}\text{ }..........\left( 3 \right) \\
\end{align}$
Now, we will equate equation 2 and 3 and then we will get:
$\Rightarrow \dfrac{\text{Ar}\left( \text{AGB} \right)}{2}=\dfrac{\text{Ar}\left( \text{ADB} \right)}{3}$
Now, we will take 2 on the RHS, therefore:
$\begin{align}
  & \Rightarrow \text{Ar}\left( \text{AGB} \right)=2\times \dfrac{\text{Ar}\left( \text{ADB} \right)}{3} \\
 & \Rightarrow \text{Ar}\left( \text{AGB} \right)=\dfrac{2}{3}\times \text{Ar}\left( \text{ADB} \right) \\
\end{align}$
Hence, Proved.

Note: It is important to draw diagrams in questions like these for a clear understanding of the examiner. Also, students can get confused between an altitude and a median. A median is a line segment that starts from a vertex and bisects the opposite side whereas the altitude of a triangle is a line segment that starts from the vertex and meets the opposite side at right angles.