Question

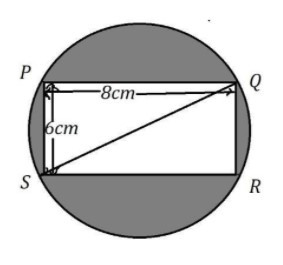
In the figure, $PQRS$ is a rectangle of $8cm \times 6cm$ inscribed in a circle. What is the area of the shaded portion?

$30.57c{m^2}$
$37.52c{m^2}$
$40.56c{m^2}$
$28.56c{m^2}$

Answer 1

Hint:We are given with the dimensions of the rectangle. Find the length of the diagonal and it will be equal to the diameter of the circle. We will get the radius from that. Now we need to calculate the area of the circle and subtract the area of the rectangle from it to get the area of the shaded region.

Complete step-by-step answer:
Let us note down the data given,
Length of the rectangle $l = 8cm$
Breadth of the rectangle $b = 6cm$

We know that the length of diagonal in a rectangle with length $l$ and breadth $b$ is $\sqrt {{l^2} + {b^2}} $.
Already we have $l = 8cm$ and $b = 6cm$. So, substitute them in the above formula, we get
Length of the diagonal $ = \sqrt {{l^2} + {b^2}} $
                    $
   = \sqrt {{8^2} + {6^2}} \\
   = \sqrt {64 + 36} \\
   = \sqrt {100} \\
   = 10 \\
 $
So, the length of the diagonal is $10cm$.
From the diagram, we can also say that the length of the diagonal of the rectangle is equal to the length of the diameter of the circle.
Hence the diameter of the circle is $10cm$.
Area of the circle with diameter $d$ is $\dfrac{{\pi {d^2}}}{4}$
Substituting the value of $d$ as $10cm$ and $\pi $ with $\dfrac{{22}}{7}$ we get,
Area of the circle $ = \dfrac{{\pi {d^2}}}{4}$
             $
   = \dfrac{{22}}{7} \times \dfrac{{{{10}^2}}}{4} \\
   = \dfrac{{550}}{7} \\
   = 78.57c{m^2} \\
 $
So, the area of the circle is $78.57c{m^2}$.
Now, area of the rectangle with length $l$ and breadth $b$ is $l \times b$
Already we have $l = 8cm$ and $b = 6cm$. So, substitute them in the above formula, we get
Area of the rectangle $ = l \times b$
                    $
   = 8 \times 6 \\
   = 48c{m^2} \\
 $
But we are asked to find out the area of the shaded region,
Area of the shaded region $ = $ Area of circle $ - $ Area of rectangle.
                    $
   = 78.57 - 48 \\
   = 30.57c{m^2} \\
 $
Hence the area of the shaded region is $30.57c{m^2}$.

So, the correct answer is “Option A”.

Note:For this kind of problem, you need to look at the figure and analyze the structures involved in it. Try to find out the dimensions of those structures. Then as per the question decide which part should be added or subtracted from the diagram to get the solution. If you are able to decide the structures, it would not be so difficult.