Question

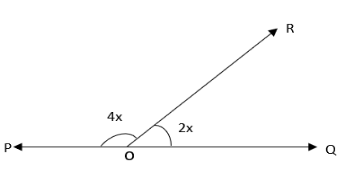
In the figure, POQ is a line, $\angle POR = 4x$ and $\angle QOR = 2x$. Find the value of x.

Answer 1

Hint: In the above question you were asked to find the value of x and two angles are given. The two angles are given in terms of x. You can solve this problem with a linear pair of an axiom. So let us see how we can solve this problem.

Complete Step by Step Solution:
It is given that POQ is a line, $\angle POR = 4x$ and $\angle QOR = 2x$ , we need to find the value of x. According to the theorem of linear pair axiom if a ray stands on a line, then the sum of two adjacent angles is ${180^ \circ }$.
 $\Rightarrow \angle POR + \angle QOR = {180^ \circ }$ (Applying the linear pair axiom theorem)
Now, we know $\angle POR = 4x$ and $\angle QOR = 2x$
So, $4x + 2x = {180^ \circ }$
 $\Rightarrow 6x = {180^ \circ }$
On dividing both sides with 6 we get,
 $\Rightarrow x = {30^ \circ }$

Therefore, the value of x is ${30^ \circ }$.

Note:
In the above solution we used linear pair axiom theorem. In linear pair axioms, when two lines intersect each other at a single point they have a combined angle of 180 degrees. You can also say these as supplementary angles.