Question

In the figure given below, PQ and RS are two mirrors placed parallel to each other. An incident ray AB strikes the mirror PQ at B, the reflected ray moves along the path BC and strikes the mirror RS at C and again reflects back along CD. Prove that AB ll CD.

Answer 1

Hint: Here, in this question, we can see that PQ and RS are the two mirrors that are placed parallel to each other. So, these two mirrors will act like the two parallel lines. And, as the mirrors PQ and RS are parallel to each other, therefore, the ray BC is acting like a transversal. So, we shall solve this question according to the result that we get when we perform any operation with the measures of the angles.
So, let us now know about the different angles formed when a transversal cuts two parallel lines. Here are some of them:
1. Corresponding Angles
2. Vertically Opposite Angles
3. Linear Pair
4. Alternate Interior Angles
5. Alternate Exterior Angles
We will then construct two normals to PQ and RS at B and C respectively. As the normals will be incident on two parallel lines, they will also be parallel to each other. We will then use the properties of the different angles formed when two parallel lines are cut by a transversal and try to prove the given condition.

Complete step-by-step answer:
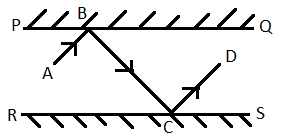
As mentioned in the question, PQ||RS. Thus, BC acts as a transversal to two parallel lines.
Now, let us construct a ‘m’ normal to PQ at B and a normal ‘n’ to RS at C.
We know that PQ||RS. Since the normals we drew are drawn to two different parallel lines, the normals will also be parallel to each other. Thus, m||n.
Now, to make it convenient, we will mark the angles at x,y,${{i}_{1}},{{i}_{2}},{{r}_{1}}$ and ${{r}_{2}}$ as shown in the figure.
Thus, our figure will look as follows:

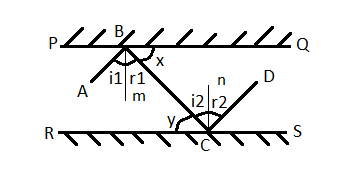
Now, if we consider the lines PQ and RS, we can see that BC is the transversal.
Here, we can see that \[\angle x\] and $\angle y$ are alternate interior angles. We also know that alternate interior angles are always equal.
Thus, $\angle x=\angle y$
Now, ‘m’ and ‘n’ are normals at PQ and RS respectively. Now, if we look at the normal ‘m’, we can see that $\angle x$ and $\angle {{r}_{1}}$ sum to ${{90}^{\circ }}$.
Thus, $\angle x+\angle {{r}_{1}}={{90}^{\circ }}$ …..(i)
Similarly, if we look at the normal ‘n’, we can see that:
$\angle y+\angle {{i}_{2}}={{90}^{\circ }}$ …..(ii)
From the equations (i) and (ii), we can see that:
$\begin{align}
  & \angle x+\angle {{r}_{1}}={{90}^{\circ }} \\
 & \Rightarrow \angle x={{90}^{\circ }}-\angle {{r}_{1}} \\
 & \angle y+\angle {{i}_{2}}={{90}^{\circ }} \\
 & \Rightarrow \angle y={{90}^{\circ }}-\angle {{i}_{2}} \\
\end{align}$
Now, we have already established that $\angle x=\angle y$,
Thus, by putting in the values of $\angle x$ and $\angle y$, we get:
$\begin{align}
  & \angle x=\angle y \\
 & \Rightarrow {{90}^{\circ }}-\angle {{r}_{1}}={{90}^{\circ }}-\angle {{i}_{2}} \\
 & \Rightarrow \angle {{r}_{1}}=\angle {{i}_{2}} \\
\end{align}$
Also, we know that the angle of incidence is equal to the angle of reflection.
Hence,
$\begin{align}
  & \angle {{i}_{1}}=\angle {{r}_{1}} \\
 & \angle {{i}_{2}}=\angle {{r}_{2}} \\
\end{align}$
Since, $\angle {{r}_{1}}=\angle {{i}_{2}}$, we can say that:
$\angle {{i}_{1}}=\angle {{r}_{1}}=\angle {{i}_{2}}=\angle {{r}_{2}}$
Since, these 4 angles are equal, the sum of any two of them will be equal to the sum of the remaining two angles.
And therefore,
$\angle {{i}_{1}}+\angle {{r}_{1}}=\angle {{i}_{2}}+\angle {{r}_{2}}$
Now, if we look at lines AB and CD, we can see that BC is a line cutting them and the sum of $\angle {{i}_{1}}$ and $\angle {{r}_{1}}$ and the sum of $\angle {{i}_{2}}$ and $\angle {{r}_{2}}$ are alternate interior angles.
Hence, AB ll CD as the alternate interior angles are equal ($\angle {{i}_{1}}+\angle {{r}_{1}}=\angle {{i}_{2}}+\angle {{r}_{2}}$).
Hence, proved.

Note: Let us now know about the different angles formed when a transversal cuts two parallel lines.

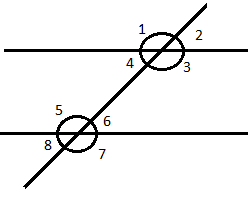
LINEAR PAIR: They are two adjacent angles which sum up to ${{180}^{\circ }}$. Here, linear pair is made by the following angles:
i. $\angle 1\text{ and }\angle 2$
ii. $\angle 4\text{ and }\angle 3$
iii. $\angle 5\text{ and }\angle 6$
iv. $\angle 7\text{ and }\angle 8$
v. $\angle 1\text{ and }\angle \text{4}$
vi. $\angle 2\text{ and }\angle 3$
vii. $\angle 5\text{ and }\angle 8$
viii. $\angle 6\text{ and }\angle 7$
VERTICALLY OPPOSITE ANGLES: they are the pair of opposite angles made when two lines intersect each other. They’re always equal. Here, pair of vertically opposite angles is formed by:
i. $\angle 1\text{ and }\angle 3$
ii. $\angle 2\text{ and }\angle 4$
iii. $\angle 5\text{ and }\angle 7$
iv. $\angle 6\text{ and }\angle 8$
CORRESPONDING ANGLES: angles in the corresponding positions on the two parallel lines with respect to the transversal are always equal. Here, pairs of corresponding angles are:
i. $\angle 1\text{ and }\angle 5$
ii. $\angle 2\text{ and }\angle 6$
iii. $\angle 4\text{ and }\angle 8$
iv. $\angle 3\text{ and }\angle 7$
ALTERNATE INTERIOR ANGLES: angles in between the parallel lines and opposite to one another, i.e. the alternate interior angles are always equal. Here, pairs of alternate interior angles are:
i. $\angle 4\text{ and }\angle 6$
ii. $\angle 5\text{ and }\angle 3$
ALTERNATE EXTERIOR ANGLES: angles outside the parallel lines and opposite to one another, i.e. the alternate exterior angles are always equal. Here, the pairs of alternate exterior angles are:
i. $\angle 1\text{ and }\angle 7$
ii. $\angle 8\text{ and }\angle 2$
CO – INTERIOR ANGLES: angles in the interior of the parallel lines on the same side of the transversal always sum up to ${{180}^{\circ }}$. Here, the pairs of co-interior angles are:
i. $\angle 4\text{ and }\angle 5$
ii. $\angle 3\text{ and }\angle 6$
CO – EXTERIOR ANGLES: angles on the exterior of the parallel lines on the same side of the transversal always up to ${{180}^{\circ }}$. Here, the pairs of co-exterior angles are:
i. $\angle 1\text{ and }\angle 8$
ii. $\angle 2\text{ and }\angle 7$
It is very important to solve this question very carefully keeping all these different types of pairs of angles in mind as if there is any mistake; the answer can come out to be wrong.