Question

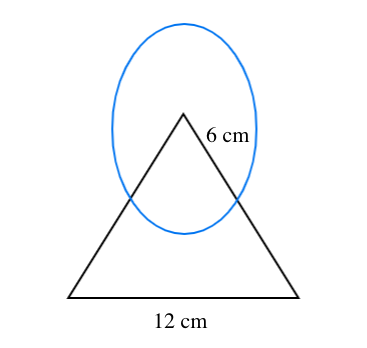
In the figure given below find the area of the shaded region where a circular arc of radius 6 cm has been drawn with vertex O of an equilateral triangle OAB of side 12 cm as center.

Answer 1

Hint: - Area of shaded region $ = $Area of circle$ + $Area of equilateral triangle$ - $area of
 common region.
Given data:
Radius of circle$\left( r \right) = 6m$
Side of an equilateral triangle$\left( a \right) = 12cm$
As we know area of circle$ = \pi {r^2} = \dfrac{{22}}{7} \times {6^2} = \dfrac{{792}}{7}c{m^2}$
Now as we know area of equilateral triangle$ = \dfrac{{\sqrt 3 }}{4}{a^2} = \dfrac{{\sqrt 3 }}{4} \times
 {12^2} = 36\sqrt 3 c{m^2}$
Area of common region (i.e. between circle and equilateral triangle)
$ \Rightarrow \left( {\dfrac{\theta }{{{{360}^0}}}} \right)\pi {r^2}$
As we know in equilateral triangles all angles equal to${60^0}$.
\[ \Rightarrow \angle {\text{AOB}} = {60^0} = \theta \]
Therefore area of common region$ = \left( {\dfrac{\theta }{{{{360}^0}}}} \right)\pi {r^2} =
 \dfrac{{{{60}^0}}}{{{{360}^0}}} \times \dfrac{{22}}{7} \times {6^2} = \dfrac{{132}}{7}c{m^2}$
Therefore, the area of the shaded region$\left( A \right)$$ = $Area of circle$ + $Area of equilateral

 triangle$ - $area of the common region.
$ \Rightarrow \left( A \right) = \dfrac{{792}}{7} + 36\sqrt 3 - \dfrac{{132}}{7} = \left( {\dfrac{{660}}{7} +
 36\sqrt 3 } \right)c{m^2}$
So, this is the required answer.

Note: -In such types of questions always remember the formula of area of standard shapes which is
 stated above, then first find out the area of circle then find out the area of triangle then find out the
 area of common region, then find out the area of shaded region using the formula which is stated above
 then simplify we will get the required answer.