Question

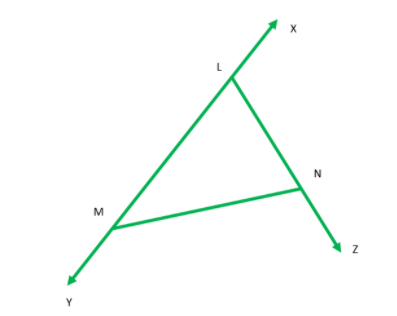
In the figure, $\angle XLN = {100^ \circ }$, \[\angle YMN = {165^ \circ }\] and $\angle ZNM = {95^ \circ }$ find the measure of $\angle MLN$.
A. 80$^ \circ $
B. 15$^ \circ $
C. 70$^ \circ $
D. 60$^ \circ $

Answer 1

Hint: We will find the angles inside the triangle using the property of supplementary angles which states that the angles on a line when added together gives 180$^ \circ $.

Complete step-by-step solution:
We see that XY is a straight line. So, we will have a pair of supplementary angles over it that is Sum of these angles result in 180$^ \circ $. These are also known as Linear pairs of Angles.
$\angle XLN + \angle MLN = {180^ \circ }$ ………...…(1)
$\angle YMN + \angle NML = {180^ \circ }$
Since, we already have the measure of $\angle XLN$ .
We won’t have to use the other equation because what we need lies in (1).
Putting this value in (1), we get:-
$\Rightarrow$${100^ \circ } + \angle MLN = {180^ \circ }$
Taking the numerical value 100 from left to right, we get:-
$\Rightarrow$$\angle MLN = {180^ \circ } - {100^ \circ } = {80^ \circ }$.
Hence, we have $\angle MLN = {80^ \circ }$.

Option A is the correct answer.

Note: We need to choose the right Linear pair. As there are three linear pairs in this question as well but we will use the one which contains the required angle. Two Angles are supplementary when they add up to 180 degrees. However, supplementary angles do not have to be on the same line, and can be separated in space. For example, adjacent angles of a parallelogram are supplementary, and opposite angles of a cyclic quadrilateral (one whose vertices all fall on a single circle) are supplementary.
If the two supplementary angles are adjacent (i.e. have a common vertex and share just one side), their non-shared sides form a straight line. Such angles are called a linear pair of angles.
We may get confused between complementary and supplementary. We need to be aware about both the terms. So, here is a way to remember and differentiate between both complementary and supplementary:- "C" of Complementary is for "Corner" right angle(a Right Angle), and "S" of Supplementary is for "Straight" (180° is a straight line).