Question

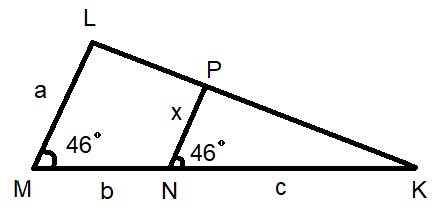
In the figure $\angle M=\angle N={{46}^{\circ }}$, express $x$ in terms of a, b and c where lengths of LM, MN and NK are a, b, c respectively. $PN=x$.

Answer 1

Hint: We first find the same angles between the $\Delta LMK$ and $\Delta PNK$. Based on the same angles we find the ratio of the similar sides. We form the relation and find the expression of $x$ in terms of a, b and c.

Complete step by step solution:
We are going to use the concept of similar triangles and use the ratio of the sides of those triangles.
In the given figure we have two triangles where we take $\Delta LMK$ and $\Delta PNK$.
It’s given that $\angle LMK=\angle PNK={{46}^{\circ }}$. Also $\angle LKM=\angle PKN$ is the common angle.
We also know that the sum of three angles of a triangle is always equal to ${{180}^{\circ }}$.
We got two angles of each triangle being equal which means the remaining angle of each triangle is also equal.
So, $\angle MLK=\angle NPK$.
We know that if three angles of two triangles are the same then the triangles are similar triangles and the ratio of opposite sides of similar angles are equal.
Therefore, for $\Delta LMK$ and $\Delta PNK$ we get $\dfrac{LM}{PN}=\dfrac{LK}{PK}=\dfrac{MK}{NK}$.
It’s given that $PN=x,LM=a,MN=b,NK=c$. Putting the values, we get
$\dfrac{LM}{PN}=\dfrac{MK}{NK}\Rightarrow \dfrac{a}{x}=\dfrac{b+c}{c}\Rightarrow x=\dfrac{ac}{b+c}$.
Expressing $x$ in terms of a, b and c we get $x=\dfrac{ac}{b+c}$.

Note:
The concept of similar triangles and congruent triangles are two different terms that are closely related. Similar triangles are two or more triangles with the same shape, equal pair of corresponding angles and the same ratio of the corresponding sides. In Euclidean geometry, two objects are similar if they have the same shape, or one has the same shape as the mirror image of the other. More precisely, one can be obtained from the other by uniformly scaling, possibly with additional translation, rotation and reflection.