Question

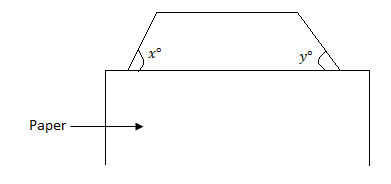
In the figure above, a shaded polygon which has equal sides and equal angles is partially covered with a sheet of blank paper. If $x + y = {80^ \circ }$. How many sides does the polygon have?

A) $Ten$
B) $Nine$
C) $Eight$
D) $Seven$
E) $Six$

Answer 1

Hint: In this problem, we have to find the number of sides in the polygon. In the given problem there is a shaded polygon which has equal sides and equal angles and is partially covered with a sheet of blank paper. In order to solve this question we have to consider that the edge of the paper forms a quadrilateral with the part of the polygon that has been shown.

Complete step-by-step answer:
As the two angles that aren’t part of the polygon add up to ${80^\circ}$, and a quadrilateral’s angles add up to ${360^\circ}$, it can be said that the angles of the polygon add up to ${280^\circ}$, and therefore each angle in the polygon is ${140^\circ}$.
Now by applying the formula of the sum of the interior angles of the polygon and dividing it by $n$ we will get the number of sides of the polygon.
$ \Rightarrow \dfrac{{(n - 2){{180}^\circ}}}{n} = {140^\circ}$
Simplifying we get,
$ \Rightarrow (n - 2){180^\circ} = 140{}^\circ$
Multiplying the terms we get,
$ \Rightarrow 180n - {360^\circ} = 140n$
Rearranging the terms and solving it for $n$ we get,
$ \Rightarrow 40n = {360^\circ}$
Hence,
$n = 9$
Hence the polygon has $9$ sides.

Thus the correct option among all is $C$.

Note: A two-dimensional shape that is bounded by a finite number of straight lines connecting in the form of a closed-loop is called a polygon. The line segments which make the polygon are known as polygon’s sides or edges. On the other hand the corner or the point where any two sides join is called the vertex of the polygon.
Polygons are classified into various types based on the number of sides and measures of the angles. They are: Regular Polygons, Irregular Polygons, Concave Polygons, Convex Polygons Trigons, Quadrilateral Polygons, Pentagon Polygons, Hexagon Polygons, Equilateral Polygons, and Equiangular Polygons.