Question

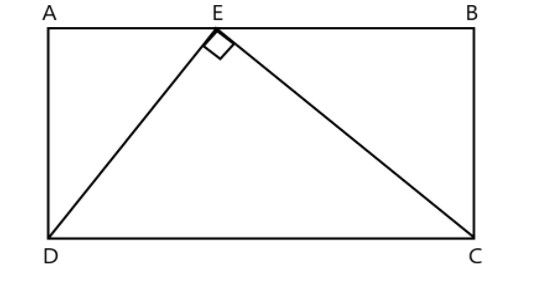
: In the diagram \[ABCD\] is a rectangle and point \[E\] lies on \[AB\]. Triangle \[DEC\] has \[\left| \!{\underline {
  {DEC} }} \right. = {90^ \circ }\], \[DE = 3\] and \[EC = 4\]. The length of \[AD\] is

A.2.4
B.2.8
C.1.8
D.3.2

Answer 1

Hint: Here in this question, we have to find the length of the side AD in the given rectangular diagram AD, this can be solve by applying a Pythagoras theorem i.e., \[hy{p^2} = op{p^2} + ad{j^2}\] in triangles \[\Delta DEC\], \[\Delta EAD\], and \[\Delta EBC\] then further simplify by using a basic arithmetic operation we get the required length of the side AD.

Complete step-by-step answer:
Consider the given diagram \[ABCD\] is a rectangular and point E lies on the side AB, and the given line DE and EC which have a length 3 and 4 respectively and the point E makes angle \[{90^ \circ }\].
In rectangle \[ABCD\], we found three triangles i.e., \[\Delta DEC\], \[\Delta EAD\] and \[\Delta EBC\]. E be the common point in all three triangles.
Now, consider the triangle \[\Delta DEC\] is a right-angled triangle.
In \[\Delta DEC\], \[\left| \!{\underline {
  E }} \right. = {90^ \circ }\]
Then by the Pythagoras theorem
\[ \Rightarrow {\left( {DC} \right)^2} = {\left( {DE} \right)^2} + {\left( {EC} \right)^2}\]
Given, \[DE = 3\] and \[EC = 4\], on substituting we have
\[ \Rightarrow {\left( {DC} \right)^2} = {\left( 3 \right)^2} + {\left( 4 \right)^2}\]
\[ \Rightarrow {\left( {DC} \right)^2} = 9 + 16\]
\[ \Rightarrow {\left( {DC} \right)^2} = 25\]
Taking square root on both side, then
\[ \Rightarrow DC = \pm \sqrt {25} \]
\[ \Rightarrow DC = \pm 5\]
When, measuring the length of any shape we only consider the positive value
\[\therefore DC = 5\]
Now, consider triangle \[\Delta EAD\] is a right-angle triangle
In, \[\Delta EAD\], \[\left| \!{\underline {
  A }} \right. = {90^ \circ }\]and let take \[AE = x\]
Then by the Pythagoras theorem
\[ \Rightarrow {\left( {DE} \right)^2} = {\left( {AD} \right)^2} + {\left( {AE} \right)^2}\]
\[ \Rightarrow {\left( 3 \right)^2} = {\left( {AD} \right)^2} + {\left( x \right)^2}\]
\[ \Rightarrow 9 = {\left( {AD} \right)^2} + {x^2}\]
On rearranging, we have
\[ \Rightarrow {\left( {AD} \right)^2} = 9 - {x^2}\]-------(1)
Now, consider triangle \[\Delta EBC\] is a right-angle triangle
In, \[\Delta EBC\], \[\left| \!{\underline {
  B }} \right. = {90^ \circ }\] and
Let, \[EB = AB - AE\]
But \[AB = DC = 5\], then
\[ \Rightarrow EB = 5 - x\]
Then by the Pythagoras theorem
\[ \Rightarrow {\left( {EC} \right)^2} = {\left( {BC} \right)^2} + {\left( {EB} \right)^2}\]
But \[BC = AD\], then
\[ \Rightarrow {\left( 4 \right)^2} = {\left( {AD} \right)^2} + {\left( {5 - x} \right)^2}\]
\[ \Rightarrow 16 = {\left( {AD} \right)^2} + {\left( {5 - x} \right)^2}\]
On applying a algebraic identity: \[{\left( {a - b} \right)^2} = {a^2} + {b^2} - 2ab\], then
\[ \Rightarrow 16 = {\left( {AD} \right)^2} + {5^2} + {x^2} - 10x\]
\[ \Rightarrow 16 = {\left( {AD} \right)^2} + 25 + {x^2} - 10x\]
On rearranging, we have
\[ \Rightarrow {\left( {AD} \right)^2} = 16 - 25 - {x^2} + 10x\]
\[ \Rightarrow {\left( {AD} \right)^2} = 10x - 9 - {x^2}\] ------(2)
From equation (1) and (2), we have
\[ \Rightarrow 9 - {x^2} = 10x - 9 - {x^2}\]
Take variable \[x\] terms in to the LHS, then
\[ \Rightarrow {x^2} - {x^2} - 10x = - 9 - 9\]
On simplification, we have
\[ \Rightarrow - 10x = - 18\]
Divide both side by -10, then we get
\[ \Rightarrow x = \dfrac{{ - 18}}{{ - 10}}\]
\[ \Rightarrow x = 1.8\]
Substitute \[x\] value in equation (1), then
\[ \Rightarrow {\left( {AD} \right)^2} = 9 - {\left( {1.8} \right)^2}\]
\[ \Rightarrow {\left( {AD} \right)^2} = 9 - 3.24\]
\[ \Rightarrow {\left( {AD} \right)^2} = 5.76\]
Take square root on both side, we have
\[ \Rightarrow AD = \pm \sqrt {5.76} \]
\[ \Rightarrow AD = \pm 2.4\]
\[\therefore AD = 2.4\]
Hence, the length of the side \[AD = 2.4\].
Therefore, Option (A) is correct.
So, the correct answer is “Option A”.

Note: To solve rectangular based problems, remember the properties of triangle i.e., the parallel sides are equal and when triangle is right angle it‘s obey the Pythagoras theorem which stated as “In a right-angled triangle, the square of the hypotenuse side is equal to the sum of squares of the other two sides” i.e., \[hy{p^2} = op{p^2} + ad{j^2}\], and main thing is measurement of length of any shape should be in positive.