Answer
385.5k+ views
Hint: We use the property that the angle opposite the greater side is greater, which gives $\angle PQR>\angle PRQ$ . We now compare the two triangles $\Delta PQS$ and $\Delta PSR$ . One of the angles of the two triangles being the same and one angle being greater than the other $\left( \angle PQR>\angle PRQ \right)$ , we must then have the remaining angle smaller than the other of the second triangle.
Complete step by step answer:
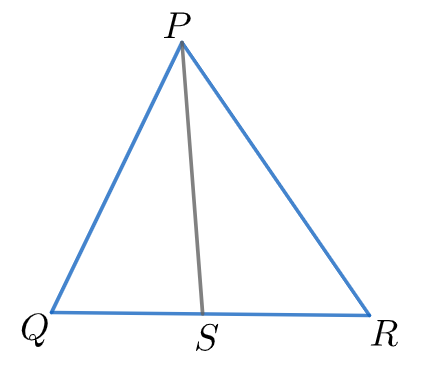
Let us start off the solution by saying that $PS$ is an angular bisector and it bisects $\angle QPR$ . This means that
$\angle QPS=\angle SPR....\left( 1 \right)$
Also, we are given that $PR>PQ$ . We know that in a triangle, the side opposite the greater angle is greater. In reverse, it can be said that the angle opposite the greater side is greater in a triangle. In this triangle $\Delta PQR$ , outside of sides $PQ$ and $PR$ , $PR$ is the greater side. The angle opposite to side $PR$ is $\angle PQR$ . This means that
$\angle PQR>\angle PRQ....\left( 2 \right)$
We know the property of a triangle that the sum of all the internal angles of a triangle is equal to ${{180}^{\circ }}$ . This means that the sum of internal angles of $\Delta PQS$ and $\Delta PRS$ separately are ${{180}^{\circ }}$ . This means,
$\angle PQS+\angle PSQ+\angle QPS={{180}^{\circ }}....\left( 3 \right)$
And
$\angle PRS+\angle PSR+\angle SPR={{180}^{\circ }}....\left( 4 \right)$
By $\left( 3 \right)$ and $\left( 4 \right)$ , we can say that
$\Rightarrow \angle PQS+\angle PSQ+\angle QPS=\angle PRS+\angle PSR+\angle SPR$
By $\left( 1 \right)$ , we can cancel the last terms from both the sides of the equation. The equation thus becomes,
$\Rightarrow \angle PQS+\angle PSQ=\angle PRS+\angle PSR$
We now subtract $\angle PRS$ from both sides of the above equation, We get,
$\Rightarrow \angle PQS-\angle PRS+\angle PSQ=\angle PSR$
We now subtract $\angle PSQ$ from both sides of the above equation, We get,
$\Rightarrow \angle PQS-\angle PRS=\angle PSR-\angle PSQ$
By $\left( 2 \right)$ we can say that the left hand side of the above equation is positive. This means that the right hand side of the above equation is also positive. For the right hand side to be positive, $\angle PSR>\angle PSQ$ .
Therefore, it has been proved that $\angle PSR>\angle PSQ$ .
Note: In these problems, the most common problem that students face is that they cannot find out how to start the problem. An easy way for it is to observe the given conditions and find out, which property is related to these conditions. We also make mistakes while naming the angles and so, we should be careful here.
Complete step by step answer:
Let us start off the solution by saying that $PS$ is an angular bisector and it bisects $\angle QPR$ . This means that
$\angle QPS=\angle SPR....\left( 1 \right)$
Also, we are given that $PR>PQ$ . We know that in a triangle, the side opposite the greater angle is greater. In reverse, it can be said that the angle opposite the greater side is greater in a triangle. In this triangle $\Delta PQR$ , outside of sides $PQ$ and $PR$ , $PR$ is the greater side. The angle opposite to side $PR$ is $\angle PQR$ . This means that
$\angle PQR>\angle PRQ....\left( 2 \right)$
We know the property of a triangle that the sum of all the internal angles of a triangle is equal to ${{180}^{\circ }}$ . This means that the sum of internal angles of $\Delta PQS$ and $\Delta PRS$ separately are ${{180}^{\circ }}$ . This means,
$\angle PQS+\angle PSQ+\angle QPS={{180}^{\circ }}....\left( 3 \right)$
And
$\angle PRS+\angle PSR+\angle SPR={{180}^{\circ }}....\left( 4 \right)$
By $\left( 3 \right)$ and $\left( 4 \right)$ , we can say that
$\Rightarrow \angle PQS+\angle PSQ+\angle QPS=\angle PRS+\angle PSR+\angle SPR$
By $\left( 1 \right)$ , we can cancel the last terms from both the sides of the equation. The equation thus becomes,
$\Rightarrow \angle PQS+\angle PSQ=\angle PRS+\angle PSR$
We now subtract $\angle PRS$ from both sides of the above equation, We get,
$\Rightarrow \angle PQS-\angle PRS+\angle PSQ=\angle PSR$
We now subtract $\angle PSQ$ from both sides of the above equation, We get,
$\Rightarrow \angle PQS-\angle PRS=\angle PSR-\angle PSQ$
By $\left( 2 \right)$ we can say that the left hand side of the above equation is positive. This means that the right hand side of the above equation is also positive. For the right hand side to be positive, $\angle PSR>\angle PSQ$ .
Therefore, it has been proved that $\angle PSR>\angle PSQ$ .
Note: In these problems, the most common problem that students face is that they cannot find out how to start the problem. An easy way for it is to observe the given conditions and find out, which property is related to these conditions. We also make mistakes while naming the angles and so, we should be careful here.
Recently Updated Pages
How many sigma and pi bonds are present in HCequiv class 11 chemistry CBSE

Why Are Noble Gases NonReactive class 11 chemistry CBSE

Let X and Y be the sets of all positive divisors of class 11 maths CBSE

Let x and y be 2 real numbers which satisfy the equations class 11 maths CBSE

Let x 4log 2sqrt 9k 1 + 7 and y dfrac132log 2sqrt5 class 11 maths CBSE

Let x22ax+b20 and x22bx+a20 be two equations Then the class 11 maths CBSE

Trending doubts
Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

At which age domestication of animals started A Neolithic class 11 social science CBSE

Which are the Top 10 Largest Countries of the World?

Give 10 examples for herbs , shrubs , climbers , creepers

Difference between Prokaryotic cell and Eukaryotic class 11 biology CBSE

Difference Between Plant Cell and Animal Cell

Write a letter to the principal requesting him to grant class 10 english CBSE

Change the following sentences into negative and interrogative class 10 english CBSE

Fill in the blanks A 1 lakh ten thousand B 1 million class 9 maths CBSE