Question

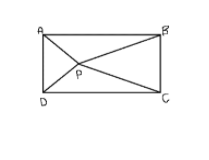
In given fig P is a point in the interior of a rectangle ABCD. Show that:
(1) $ar\left( {APB} \right) + ar\left( {CPD} \right) = \dfrac{1}{2}ar\left( {ABCD} \right)$
(2) $ar\left( {APD} \right) + ar\left( {BPC} \right) = ar\left( {APB} \right) + ar\left( {CPD} \right)$

Answer 1

Hint: Draw a line passing through $P$ and parallel to side $AD$ cutting the sides $AB$ and $CD$ at $E$ and $F$ respectively.

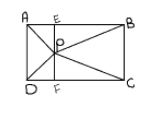
Then, find the area of Triangles $APB$ and $CPD$ by using the formula $area = \dfrac{1}{2} \times B \times H$ where $B$ is the base and $H$ is the height of the triangle. Then, add the area of both triangles. And compare it with the area of the rectangle.

Complete step by step answer:
Given, ABCD is a rectangle and area of rectangle $ABCD = AB \times AD$
($\because $ area of rectangle $ = $ length $ \times $ breadth)
Now, In triangle $APB$, $AB$ is the base of the triangle and $EP$ is the height of the triangle because $EP$ is perpendicular to $AB$.
So, area of triangle $APB = \dfrac{1}{2} \times AB \times EP$
Similarly, In triangle $CPD$, $CD$ is the base of the triangle and $FP$ is the height of the triangle.
So, area of triangle $CPD = \dfrac{1}{2} \times CD \times FP$
Now, adding the area of both triangles we get,
$\Rightarrow ar\left( {APB} \right) + ar\left( {CPD} \right) = \left( {\dfrac{1}{2} \times AB \times EP} \right) + \left( {\dfrac{1}{2} \times CD \times FP} \right)$
Taking $\dfrac{1}{2}$ common from both in right hand side we get,
$\Rightarrow ar\left( {APB} \right) + ar\left( {CPD} \right) = \dfrac{1}{2} \times \left( {\left( {AB \times EP} \right) + \left( {CD \times FP} \right)} \right)$
Since $ABCD$ is a rectangle so opposite sides are equal.
$\therefore AB = CD$
$\Rightarrow ar\left( {APB} \right) + ar\left( {CPD} \right) = \dfrac{1}{2} \times \left( {\left( {AB \times EP} \right) + \left( {AB \times FP} \right)} \right)$
Taking $AB$ common from both we get,
$\Rightarrow ar\left( {APB} \right) + ar\left( {CPD} \right) = \dfrac{1}{2} \times AB \times \left( {EP + FP} \right)$
From figure it is obvious that $EF = EP + FP$
$\therefore ar\left( {APB} \right) + ar\left( {CPD} \right) = \dfrac{1}{2} \times AB \times EF$
Now in rectangle $ABCD$, $AD = EF = BC$ because opposite sides are equal and parallel.
Thus, we can write
$\Rightarrow ar\left( {APB} \right) + ar\left( {CPD} \right) = \dfrac{1}{2} \times AB \times AD$
Since $ar\left( {ABCD} \right) = AB \times AD$ proved above.
We can finally write $ar\left( {APB} \right) + ar\left( {CPD} \right) = ar\left( {ABCD} \right)$

Hence, (1) is proved.

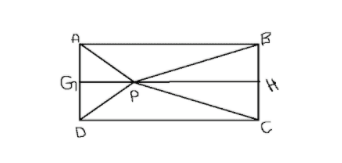
(2) Draw a line passing through $P$ and parallel to $AB$ then find the area of triangles $APD$ and $BPC$ using formula $area = \dfrac{1}{2} \times B \times H$ where $B$ is the base and $H$ is the height of the triangle. Then, add the area of both triangles.

Given, ABCD is a rectangle and area of rectangle $ABCD = AB \times AD$
($\because $ area of rectangle $ = $ length $ \times $ breadth)
Now, In triangle $APD$, $AD$ is the base of triangle and $GP$ is the height of triangle because $GP$ is perpendicular to $AD$.
So, area of triangle $APD = \dfrac{1}{2} \times AD \times GP$
Similarly, In triangle $BPC$, $BC$ is the base of the triangle and $HP$ is the height of the triangle.
So, area of triangle $BPC = \dfrac{1}{2} \times BC \times HP$
Now, adding the area of both triangles we get,
$\Rightarrow ar\left( {APD} \right) + ar\left( {BPC} \right) = \left( {\dfrac{1}{2} \times AD \times GP} \right) + \left( {\dfrac{1}{2} \times BC \times HP} \right)$
Taking $\dfrac{1}{2}$ common from both in right hand side we get,
$\Rightarrow ar\left( {APD} \right) + ar\left( {BPC} \right) = \dfrac{1}{2} \times \left( {\left( {AD \times GP} \right) + \left( {BC \times HP} \right)} \right)$
Since,$ABCD$ is a rectangle so opposite sides are equal.
$\therefore AD = {\rm B}C$
$\Rightarrow ar\left( {APD} \right) + ar\left( {BPC} \right) = \dfrac{1}{2} \times \left( {\left( {AD \times GP} \right) + \left( {AD \times HP} \right)} \right)$
Taking $AD$ common from both we get,
$\Rightarrow ar\left( {APD} \right) + ar\left( {BPC} \right) = \dfrac{1}{2} \times AD \times \left( {GP + {\rm H}P} \right)$
From figure it is obvious that $GH = GP + HP$
$\therefore ar\left( {APD} \right) + ar\left( {BPC} \right) = \dfrac{1}{2} \times AD \times GH$
Now in rectangle $ABCD$, $AB = CD = GH$ because opposite sides are equal and parallel.
Thus, we can write
$\Rightarrow ar\left( {APD} \right) + ar\left( {BPC} \right) = \dfrac{1}{2} \times AD \times AB$
Since $ar\left( {ABCD} \right) = AB \times AD$ proved above.
We can finally write $ar\left( {APD} \right) + ar\left( {BPC} \right) = ar\left( {ABCD} \right)$
Since the right side of the result of (1) and of this are equal so, we can equate the left-hand side then,
$\Rightarrow ar\left( {APB} \right) + ar\left( {CPD} \right) = ar\left( {APD} \right) + ar\left( {BPC} \right) = \dfrac{1}{2}ar\left( {ABCD} \right)$

Hence, (2) is proved.

Note:
- In this type of problem make suitable construction which converts the given figure into a known figure whose area and perimeter can be written easily
- If the right-hand side of two equations is equal then we can say that the left-hand side must be equal.
- This relation is also valid in the case of a square.