Question

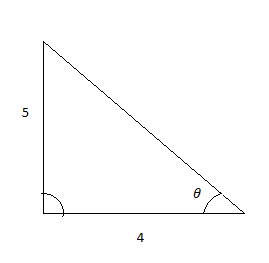
In figure, calculate the value of \[\theta \]
$A){\text{ }}36.9_{}^0$
$B){\text{ }}38.6_{}^0$
$C){\text{ }}41.4_{}^0$
$D){\text{ }}47.2_{}^0$
$E){\text{ }}51.3_{}^0$

Answer 1

Hint: To solve this question we can apply the formula, of $\tan \theta $, and then we will get the required value of $\theta $ after doing inverse at last to get the required answer.

Formula used:
$\tan \theta = \dfrac{{Perpendicular}}{{Base}}$.

Complete step by step answer:
From the above diagram, we can see that the value of the perpendicular is $5$ and the value of the base is $4$.
Now by applying the formula $\tan \theta = \dfrac{{Perpendicular}}{{Base}}$ we get-
$\tan \theta = \dfrac{5}{4}$
$\Rightarrow \theta = {\tan ^{ - 1}}\left( {\dfrac{5}{4}} \right)$
$\Rightarrow \theta = 51.3_{}^0$

$\therefore$ The required value of $\theta $ is $51.3_{}^0$. Thus the correct option is $E$.

Note:
It is to be kept in mind that there are several formulas of $\tan \theta $ and most of the students make mistakes in applying the correct formula so try to remember all the formulas.
Another formula of $\tan \theta = \dfrac{{\sin \theta }}{{\cos \theta }}$or $\tan \theta = \sqrt {\sec _{}^2\theta - 1} $
There are three sides in a triangle and each side represents either perpendicular or base or hypotenuse. So when the values of perpendicular and hypotenuse are given, then we can find out the value of $\theta $ by using the formula$\sin \theta = \dfrac{{Perpendicular}}{{Hypotenuse}}$. Other formulas for finding out the values of $\theta $ is $\sin \theta = \sqrt {1 - \cos _{}^2\theta } $
When the values of base and hypotenuse are given then we can find out the value of $\theta $by using the formula of $\cos \theta $$ = \dfrac{{Base}}{{Hypotenuse}}$. Other formula for finding out the value of $\cos \theta $ is $\cos \theta = \sqrt {1 - \sin _{}^2\theta } $
When the values of perpendicular and base are given, then we can find out the value of $\theta $ by using the formula of $\tan \theta = \dfrac{{Perpendicular}}{{Base}}$.
If the values of perpendicular, base, and height or any two of them are given in the question, then to find out the angle we will apply the formula of $\sin \theta $, $\cos \theta $ or $\tan \theta $