Question

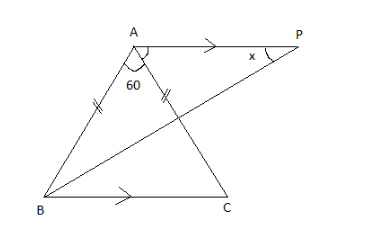
In figure
BP bisects \[\angle ABC\] and AB=AC. Find x

Find x in figure (ii).
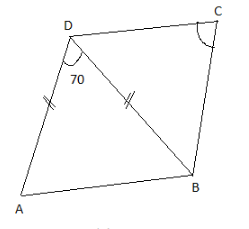
Given: DA=DB=DC, BD bisects \[\angle ABC\] and \[\angle ADB = {70^ \circ }\]

Answer 1

Hint: In this question, we need to determine the value of the angle denoted by ‘x’. For this, we will first find all the angles of the triangle and by using angle bisector we will find the bisected angles and then we will find the required angle

Complete step-by-step answer:

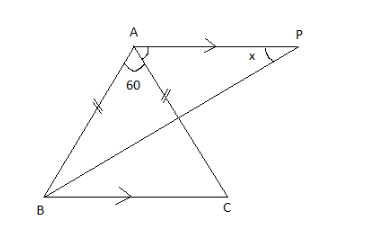
Given in the figure (i), in triangle ABC the side AB=AC
Now since we know that the angles opposite to equal sides are equal, hence we can say \[\Rightarrow \angle ABC = \angle ACB\]
Let us assume that \[\angle ABC = \angle ACB = k\]
Now since we know that the sum of internal angles of a triangle is equal to 180 degree, hence we can say
\[\Rightarrow \angle ABC + \angle ACB + \angle BAC = {180^ \circ }\]
By substituting the values in the equation, we get
\[
\Rightarrow k + k + {60^ \circ } = {180^ \circ } \\
\Rightarrow 2k = {180^ \circ } - {60^ \circ } \\
\Rightarrow k = \dfrac{{{{120}^ \circ }}}{2} \\
\Rightarrow k = {60^ \circ } \\
 \]
\[\therefore \angle ABC = \angle ACB = {60^ \circ }\]
Now since the line BP is the angle bisector of the\[\angle ABC\], so\[\angle ABP = \angle PBC\]
Hence we can write
\[\Rightarrow \angle ABP = \angle PBC = \dfrac{{\angle ABP}}{2} = {30^ \circ }\]
We can see that the line AP is parallel to the line BC so by using the alternate interior angle theorem we can say
\[\Rightarrow \angle PBC = \angle BPA\]
Hence we can say
\[\Rightarrow \angle PBC = \angle BPA = {30^ \circ }\]
Therefore
 \[x = {30^ \circ }\] Answer.
So, the correct answer is “ \[x = {30^ \circ }\]”.


ii. Now considering the figure (ii),

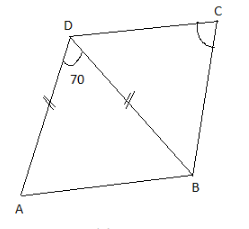
Given the side DA=DB=DC
In triangle ADB the side AB=AC
Now since we know that the angles opposite to equal sides are equal, hence we can say \[\Rightarrow \angle DAB = \angle DBA\]
Let us assume that \[\angle DAB = \angle DBA = z\]
Now since we know that the sum of internal angles of a triangle is equal to 180 degree, hence we can say
\[\Rightarrow \angle DAB + \angle DBA + \angle ADB = {180^ \circ }\]
By substituting the values in the equation, we get
\[
\Rightarrow z + z + {70^ \circ } = {180^ \circ } \\
\Rightarrow 2k = {180^ \circ } - {70^ \circ } \\
\Rightarrow k = \dfrac{{{{110}^ \circ }}}{2} \\
\Rightarrow k = {55^ \circ } \\
 \]
\[\therefore \angle DAB = \angle DBA = {55^ \circ }\]
Now since the line BD is the angle bisector of the\[\angle ABC\], so\[\angle ABD = \angle CBD\]
Hence we can write
\[\angle ABC = \angle DBC = \dfrac{{\angle ABC}}{2} = {27.5^ \circ }\]
Now it is also given that line DB=DC and as we know that the angles opposite to equal sides are equal, hence we can say \[\angle DBC = \angle DCB\]
Hence we can say
\[\angle DBC = \angle DCB = {27.5^ \circ }\]
Therefore, \[x = {27.5^ \circ }\]
So, the correct answer is “\[x = {27.5^ \circ }\]”.

Note: The sum of the internal angles of a triangle is equal to 180 degree and if the three angles of the triangle are equal then the triangle is equilateral triangle. Students must note that when a line is drawn touching the two parallel lines then their alternate angles on both the lines are equal.