Question

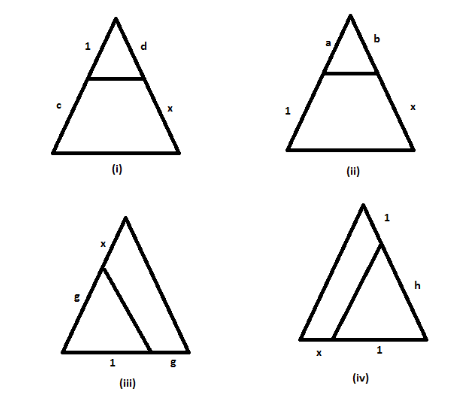
In each of the figures, a line segment is drawn parallel to one side of the triangle and the lengths of certain line segments are marked. Find the value of $X$ in each of the following:

Answer 1

Hint: First we have to see the figure clearly.
The line divides the triangle into two proportions.
The side of triangles has values.
From the given triangle, we get the values and then we applied in proportionality theorem
Finally, we can find the value of $X$.

Formula used: Triangle proportionality theorem: If a line parallel to one side of a triangle intersects the other sides, then it divides those sides proportionally.

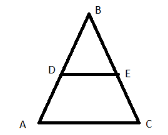
If $\overline {DE} $ is parallel to $\overline {AC} $, then $\dfrac{{BD}}{{DA}} = \dfrac{{BE}}{{EC}}$

Complete step-by-step answer:
In this figure a line segment is drawn parallel to one side of the triangle and the lengths of certain line segments are marked.
(i) In the triangle applying proportionality theorem on their sides we get,
\[\dfrac{1}{c} = \dfrac{d}{{\mathbf{x}}}\]
By Cross multiplication we get,
\[ \Rightarrow {\mathbf{x}} = cd\]
Therefore, the value of $X$ is \[cd\]
(ii) In the triangle applying proportionality theorem on their sides we get,
\[\dfrac{a}{1} = \dfrac{b}{{\mathbf{x}}}\]
By Cross multiplication we get
\[ \Rightarrow {\mathbf{x}} = \dfrac{b}{a}\]
Therefore, the value of $X$ is \[\dfrac{b}{a}\]
(iii) In the triangle applying proportionality theorem on their sides we get,
\[\dfrac{1}{g} = \dfrac{g}{{\mathbf{x}}}\]
By Cross multiplication we get
\[ \Rightarrow {\mathbf{x}} = {g^2}\]
Therefore, the value of $X$ is \[{g^2}\]
(iv) In the triangle applying proportionality theorem on their sides we get,
\[\dfrac{1}{{\mathbf{x}}} = \dfrac{h}{1}\]
By Cross multiplication we get,
\[ \Rightarrow {\mathbf{x}} = \dfrac{1}{h}\]
Therefore, the value of $X$ is \[\dfrac{1}{h}\]

Note: The converse of the proportionality theorem is also true.
If a line divides two sides of a triangle proportionally then it is parallel to the third side of the triangle.
If $\dfrac{{BD}}{{DA}} = \dfrac{{BE}}{{EC}}$ then,$\overline {DE} $ is parallel to $\overline {AC} $.