Question

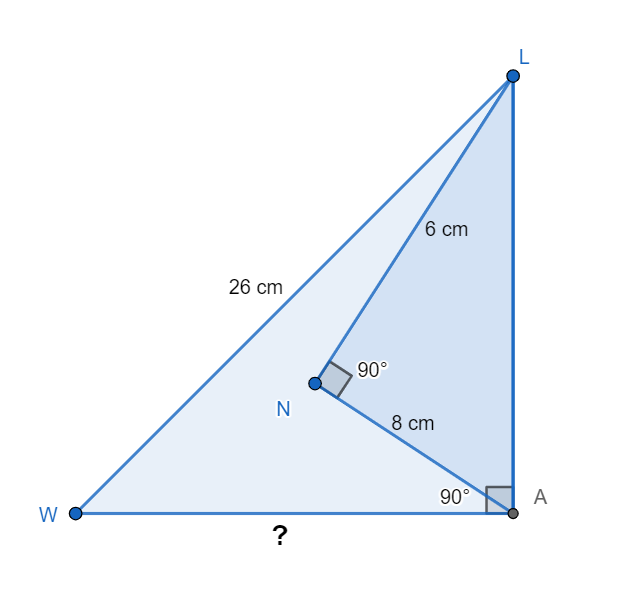
In \[\Delta LAW\], \[\angle LAW=90{}^\circ \], \[\angle LNA=90{}^\circ \], LW=26 cm, LN=6 cm and AN=8 cm. Calculate the length of WA.

Answer 1

Hint: This question is from the topic of triangles. In solving this question, we are going to use Pythagoras theorem. We will first find the length of side LA using Pythagoras theorem in the triangle LAN. After that, we will find the length of side WA using the Pythagoras theorem in the triangle LAW using the given sides and angles.

Complete step by step answer:
Let us solve this question.
In this question, we can see from the diagram that there are two triangles that are triangle LAW and triangle LAN, in which sides are given as
LW= 26 cm
LN= 6 cm
AN= 8 cm
And angles are given as
\[\angle LAW=90{}^\circ \]
\[\angle LNA=90{}^\circ \]
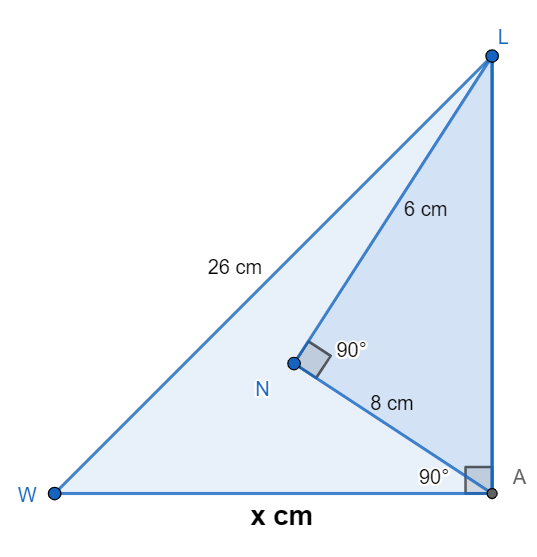
Let the length of WA that we have to find be x cm.

In triangle LAN, using Pythagoras theorem, we can write
\[{{\left( LA \right)}^{2}}={{\left( AN \right)}^{2}}+{{\left( LN \right)}^{2}}\]
Putting the values of AN and LN as 8 cm and 6 cm respectively, we will get
\[\Rightarrow {{\left( LA \right)}^{2}}={{\left( 8 \right)}^{2}}+{{\left( 6 \right)}^{2}}=64+36=100\]
We can write the above equation as
\[\Rightarrow {{\left( LA \right)}^{2}}={{\left( 10 \right)}^{2}}\]
On squaring root both sides of the equation, we get
\[\Rightarrow \sqrt{{{\left( LA \right)}^{2}}}=\sqrt{{{\left( 10 \right)}^{2}}}\]
The above equation can also be written as
\[\Rightarrow LA=10\]
Hence, we get that length of side LA is 10 cm.
Now, using Pythagoras theorem in the triangle LAW, we can write
\[{{\left( LW \right)}^{2}}={{\left( WA \right)}^{2}}+{{\left( LA \right)}^{2}}\]
Putting the value of WA as x, the value of LW as 26 cm and the value of LA as 10 cm in the above equation, we get
\[\Rightarrow {{\left( 26 \right)}^{2}}={{\left( x \right)}^{2}}+{{\left( 10 \right)}^{2}}\]
We can write the above equation as
\[\Rightarrow 676={{\left( x \right)}^{2}}+100\]
The above equation can also be written as
\[\Rightarrow {{\left( x \right)}^{2}}=676-100\]
\[\Rightarrow {{\left( x \right)}^{2}}=576\]
Now, squaring root on both sides of the equation, we get
\[\Rightarrow \sqrt{{{\left( x \right)}^{2}}}=\sqrt{576}=\sqrt{{{24}^{2}}}\]
\[\Rightarrow x=24\]
As we have taken WA as x, so we can say that the value of WA is 24.

Hence, the length of side WA is 24.

Note: We should have better knowledge in the topic of triangles for solving this type of question. We should know about the Pythagoras theorem for solving this type of question easily. The Pythagoras theorem states that in a right angled triangle, the square of the hypotenuse side is always equal to the sum of squares of the other two sides. The hypotenuse side is always the longest side, and it is opposite to the angle of 90 degrees.