Question

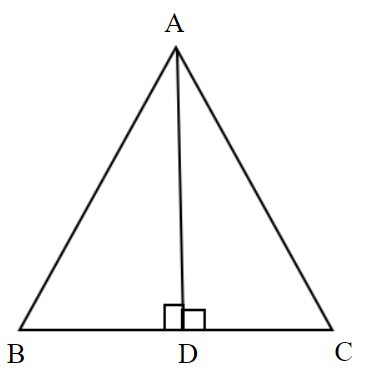
In $\Delta {\text{ABC}}$, AD is perpendicular to BC. Prove that ${\left( {{\text{AB}}} \right)^2} + {\left( {{\text{CD}}} \right)^2} = {\left( {{\text{AC}}} \right)^2} + {\left( {{\text{BD}}} \right)^2}$.

Answer 1

Hint- Here, we will be proceeding further with the help of Pythagoras theorem.

Clearly, from the figure we can see that there are total two right angled triangles $\Delta {\text{ABD}}$ and $\Delta {\text{ACD}}$.
As we know that the side opposite to the right angle in any right angled triangle is hypotenuse, the side opposite to the considered acute angle is perpendicular and the remaining side is base.
In right angled $\Delta {\text{ABD}}$, AB is a hypotenuse and in $\Delta {\text{ACD}}$, AC is a hypotenuse.
According to Pythagoras theorem, we know that
${\left( {{\text{Hypotenuse}}} \right)^2} = {\left( {{\text{Perpendicular}}} \right)^2} + {\left( {{\text{Base}}} \right)^2}$
Therefore, in right angled $\Delta {\text{ABD}}$, ${\left( {{\text{AB}}} \right)^2} = {\left( {{\text{AD}}} \right)^2} + {\left( {{\text{BD}}} \right)^2}{\text{ }} \to {\text{(1)}}$
and in right angled $\Delta {\text{ACD}}$, ${\left( {{\text{AC}}} \right)^2} = {\left( {{\text{AD}}} \right)^2} + {\left( {{\text{CD}}} \right)^2} \Rightarrow {\left( {{\text{AD}}} \right)^2} = {\left( {{\text{AC}}} \right)^2} - {\left( {{\text{CD}}} \right)^2}{\text{ }} \to {\text{(2)}}$
Using equation (2) in equation (1), we get
${\left( {{\text{AB}}} \right)^2} = {\left( {{\text{AC}}} \right)^2} - {\left( {{\text{CD}}} \right)^2} + {\left( {{\text{BD}}} \right)^2} \Rightarrow {\left( {{\text{AB}}} \right)^2} + {\left( {{\text{CD}}} \right)^2} = {\left( {{\text{AC}}} \right)^2} + {\left( {{\text{BD}}} \right)^2}$
The above equation is what we needed to prove.

Note- In these types of problems, Pythagora's theorem is to be used keeping in mind the concept of a right triangle i.e., which side is to be taken hypotenuse. Also, in the above problem the choice between perpendicular and base is flexible since that choice depends upon the acute angle considered.