Question

In any triangle, the centroid divides the median in the ratio of:
A) 1:1
B) 2:1
C) 3:1
D) 3:2

Answer 1

Hint: We will first draw a triangle and its median to get the centroid. After that, we will extend the end such that we get an inverted triangle downwards and then by the use of mid – point theorem get the required answer.

Complete step-by-step solution:
Let us first of all draw the triangle named as ABC with its medians and centroid.

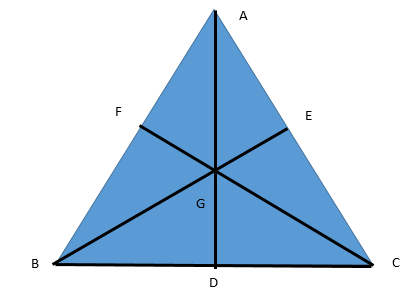
Now we will extend AD to K such that AG = GK as well as join BK and CK.
We will then get a figure looking as follows:-

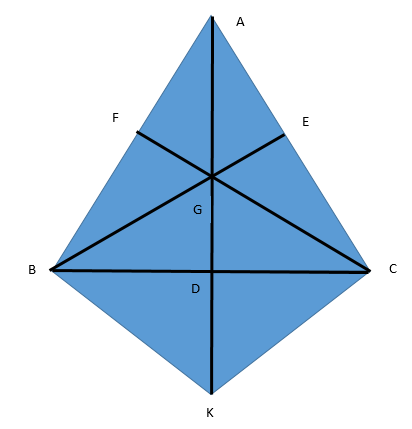
Now look at \[\vartriangle ABK\]:
Since, F and G are mid points of AB and AK respectively (Because we extended AB such that AG = GK).
$\therefore $ FG || BK (By the mid – point theorem)
Now since FG is a part of FC, therefore we will get:-
$\therefore $ GC || BK …………………(1)
Now look at \[\vartriangle ACK\]:
Since, E and G are mid points of AC and AK respectively (Because we extended AB such that AG = GK).
$\therefore $ GE || CK (By the mid – point theorem)
Now since GE is a part of BE, therefore we will get:-
$\therefore $ BG || CK …………………(2)
Now using (1) and (2), we get that:-
BGCK is a parallelogram.
We know that diagonals in a parallelogram bisect each other.
$\therefore $ GD = DK ……………….(3)
And we already have AG = GK
We can write it as follows:-
$ \Rightarrow $ AG = GD + DK
Now, on using (3), we will get the following expression:-
$ \Rightarrow $ AG = 2GD
Now, we can write this as following expression:-
$ \Rightarrow \dfrac{{AG}}{{GD}} = \dfrac{2}{1}$
$\therefore $ the centroid of the triangle divides each of its median in the ratio 2:1.

Hence, the correct option is (B).

Note: Now, let us understand the mid – point theorem which we used in the solution of the question above.
The mid – point theorem states that “the line segment in a triangle joining the midpoint of two sides of the triangle is said to be parallel to its third side and is also half of the length of the third side.”