Question

In an isosceles triangle $ABC$, with $AB = AC$, the bisectors of $\angle B = \angle C$ intersect each other at $O$.Join $A$ to $O$. Show that $(i) OB = OC $ and $(ii) AO$ bisects $\angle A$.

Answer 1

Hint: Join $A$ to $O$. Apply the given condition to the isosceles triangle and use similarity criterion.
According to given data we have 3 conditions,
$AB = AC \to (1)$
$OB$ is the bisector of $\angle B$
So,$\angle ABO = \angle OBC = \dfrac{1}{2}\angle B \to (2)$
$OC$ is the bisector of$\angle C$
So,$\angle ACO = \angle OCB = \dfrac{1}{2}\angle C$$ \to (3)$
Case-1
So, here we have to prove $OB = OC$
Proof:
 Now by using condition (1) we can say that,
 $AB = AC$
From this condition we say that
$ \Rightarrow \angle ACB = \angle ABC$ [ Where we know that Angles opposite to equal sides are equal]
$\
   \Rightarrow \dfrac{1}{2}\angle ACB = \dfrac{1}{2}\angle ABC \\
    \\
\ $
$ \Rightarrow \angle OCB = \angle OBC$ [From (2) and (3)]
Hence,
      $OB = OC$ [Sides opposite to equal angles are equal]
Hence proved that $OB = OC$.
Case-2
We have to prove that $\angle OAB = \angle OAC$
By using case (1) we know that $OB = OC$
 And also from $\Delta ABO$ and$\Delta ACO$, we have
$ \Rightarrow AB = AC$ (Given)
$ \Rightarrow AO = OA$ (Common)
$ \Rightarrow OB = OC$(From (case 1))
$\therefore \Delta ABO \cong \Delta ACO$ (By SSS Congruence rule)
$ \Rightarrow \angle OAB = \angle OAC$ (CPCPT Theorem)

Hence we have proved that$\angle OAB = \angle OAC$.

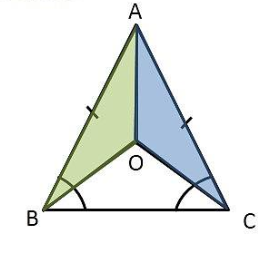
CASE - 1 CASE - 2
NOTE: In this problem given construction is mandatory to prove the given statements so join $A$ and $O$ points.