Question

In an isosceles trapezium, the length of one of the parallel sides, and the lengths of the non-parallel sides are all equal to $30$ In order to maximize the area of the trapezium, the smallest angle should be.
A.$\dfrac{\pi }{6}$
B.$\dfrac{\pi }{4}$
C.$\dfrac{\pi }{3}$
D.$\dfrac{\pi }{2}$

Answer 1

Hint: since we are given length of parallel sides and hence we should use
the area formula of parallel side and use it.

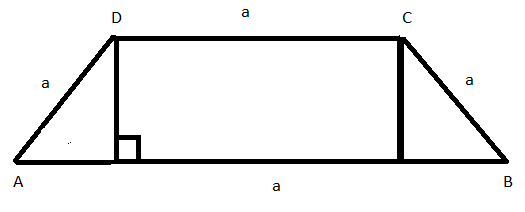
Let the angle made by hypotenuse of the right angle triangle with the base the trapezium be $\theta $
now the length of the base of the triangle is $a\cos \theta $
and the length of the perpendicular of the triangle or the distance between the
parallel sides of the trapezium is $a\sin \theta $
now the area of the trapezium = $\dfrac{1}{2}$(sum of parallel sides)$ \times $(distance between the parallel sides)
now for our given trapezium substituting the values we get
area = A=$\dfrac{1}{2} \times (a + 2a\;cos\theta + a) \times (a\;sin\theta )$
where $a = 30$
now on solving A =\[{a^2} \times (\;cos\theta + 1) \times (sin\theta )\]
on opening the brackets and using the identity $\sin 2\theta = 2\cos \theta \sin \theta $
A=\[{a^2}(\dfrac{1}{2} \times sin2\theta + \;sin\theta )\]
Now to maximize A we need to differentiate the equation for A with respect
to $\theta {\text{ and put }}\dfrac{{dA}}{{d\theta }} = 0$
now on differentiating the equation of A we get and equating it to $0$
\[(\cos 2\theta + \;\cos \theta ) = 0\]
Now using identity of $\cos 2\theta = 2{\cos ^2}\theta - 1$
And simplifying we get
\[
  2\;co{s^2}\theta + \;cos\theta - 1 = 0 \\
   \Rightarrow \cos \theta = \dfrac{1}{2}, - 1 \\
   \Rightarrow \theta = \dfrac{\pi }{3},\pi \\
\]
But since we want the smallest angle hence answer is $\dfrac{\pi }{3}$,option C
Note: while calculating questions of area of various polygons use various trigonometric formulae to simplify the calculation