Question

In an equilateral triangle ABC, D is a point on side BC such that ${\text{BD}} = \dfrac{1}{3}\left( {{\text{BC}}} \right)$. Prove that $9{\left( {{\text{AD}}} \right)^2} = 7{\left( {{\text{AB}}} \right)^2}$.

.

Answer 1

Hint- Here, we will be using Pythagoras theorem and will be converting all other sides in terms of sides AD and AB which are present in the equation which needs to be proved.
To prove- $9{\left( {{\text{AD}}} \right)^2} = 7{\left( {{\text{AB}}} \right)^2}$
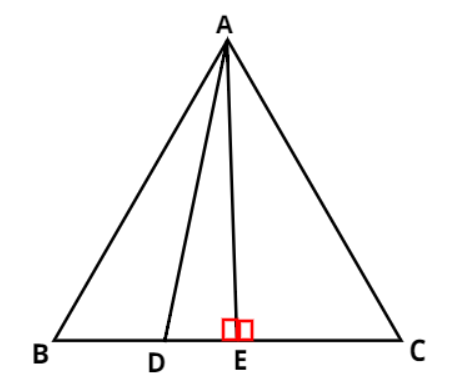
Let us draw an equilateral $\vartriangle {\text{ABC}}$ with sides AB, BC and AC equal to each other. Also, draw a line from the vertex A which will meet the side BC at point D such that ${\text{BD}} = \dfrac{1}{3}\left( {{\text{BC}}} \right)$. Also, draw a perpendicular from the vertex A on the side BC which divides line BC into two equal parts i.e., ${\text{BE}} = {\text{CE}} = \dfrac{{{\text{BC}}}}{2}$
As, ${\text{BD}} = \dfrac{1}{3}\left( {{\text{BC}}} \right){\text{ }} \to {\text{(1)}}$
Here, ${\text{AB}} = {\text{BC}} = {\text{AC}}$ and ${\text{DE}} = \left( {{\text{BE}} - {\text{BD}}} \right)$
As we know that, Pythagoras theorem states that the square of the hypotenuse is equal to the sum of the squares of perpendicular and base in a right angled triangle.
In right angled $\vartriangle {\text{ADE}}$,
Using Pythagoras theorem \[{\left( {{\text{AD}}} \right)^2} = {\left( {{\text{AE}}} \right)^2} + {\left( {{\text{DE}}} \right)^2} \Rightarrow {\left( {{\text{AD}}} \right)^2} = {\left( {{\text{AE}}} \right)^2} + {\left( {{\text{BE}} - {\text{BD}}} \right)^2}{\text{ }} \to {\text{(2)}}\]
In right angled $\vartriangle {\text{ABE}}$,
Using Pythagoras theorem \[{\left( {{\text{AB}}} \right)^2} = {\left( {{\text{AE}}} \right)^2} + {\left( {{\text{BE}}} \right)^2} \Rightarrow {\left( {{\text{AE}}} \right)^2} = {\left( {{\text{AB}}} \right)^2} - {\left( {{\text{BE}}} \right)^2} \Rightarrow {\left( {{\text{AE}}} \right)^2} = {\left( {{\text{AB}}} \right)^2} - {\left( {\dfrac{{{\text{BC}}}}{2}} \right)^2}{\text{ }} \to {\text{(3)}}\]
Now using equation (3) in equation (2), we get
\[ \Rightarrow {\left( {{\text{AD}}} \right)^2} = {\left( {{\text{AB}}} \right)^2} - {\left( {\dfrac{{{\text{BC}}}}{2}} \right)^2} + {\left( {{\text{BE}} - {\text{BD}}} \right)^2}{\text{ }}\]
Using ${\text{BE}} = \dfrac{{{\text{BC}}}}{2}$ and ${\text{BD}} = \dfrac{1}{3}\left( {{\text{BC}}} \right)$ , the above equation becomes
\[
   \Rightarrow {\left( {{\text{AD}}} \right)^2} = {\left( {{\text{AB}}} \right)^2} - {\left( {\dfrac{{{\text{BC}}}}{2}} \right)^2} + {\left( {\dfrac{{{\text{BC}}}}{2} - \dfrac{{{\text{BC}}}}{3}} \right)^2} = {\left( {{\text{AB}}} \right)^2} - \left[ {\dfrac{{{{\left( {{\text{BC}}} \right)}^2}}}{4}} \right] + {\left( {\dfrac{{{\text{3BC}} - {\text{2BC}}}}{6}} \right)^2} = {\left( {{\text{AB}}} \right)^2} - \left[ {\dfrac{{{{\left( {{\text{BC}}} \right)}^2}}}{4}} \right] + \left[ {\dfrac{{{{\left( {{\text{BC}}} \right)}^2}}}{{36}}} \right] \\
   \Rightarrow {\left( {{\text{AD}}} \right)^2} = {\left( {{\text{AB}}} \right)^2} + \left[ {\dfrac{{{{\left( {{\text{BC}}} \right)}^2}}}{{36}} - \dfrac{{{{\left( {{\text{BC}}} \right)}^2}}}{4}} \right] = {\left( {{\text{AB}}} \right)^2} + \left[ {\dfrac{{{{\left( {{\text{BC}}} \right)}^2} - 9{{\left( {{\text{BC}}} \right)}^2}}}{{36}}} \right] = {\left( {{\text{AB}}} \right)^2} + \left[ {\dfrac{{ - 8{{\left( {{\text{BC}}} \right)}^2}}}{{36}}} \right] = {\left( {{\text{AB}}} \right)^2} - \left[ {\dfrac{{2{{\left( {{\text{BC}}} \right)}^2}}}{9}} \right] \\
 \]
Also, ${\text{AB}} = {\text{BC}} = {\text{AC}} \Rightarrow {\text{BC}} = {\text{AB}}$so the above equation becomes
\[
   \Rightarrow {\left( {{\text{AD}}} \right)^2} = {\left( {{\text{AB}}} \right)^2} - \left[ {\dfrac{{2{{\left( {{\text{BC}}} \right)}^2}}}{9}} \right] = {\left( {{\text{AB}}} \right)^2} - \dfrac{{2{{\left( {{\text{AB}}} \right)}^2}}}{9} = \dfrac{{9{{\left( {{\text{AB}}} \right)}^2} - 2{{\left( {{\text{AB}}} \right)}^2}}}{9} = \dfrac{{7{{\left( {{\text{AB}}} \right)}^2}}}{9} \\
   \Rightarrow 9{\left( {{\text{AD}}} \right)^2} = 7{\left( {{\text{AB}}} \right)^2} \\
 \]
The above equation is the equation we needed to prove. Hence it is proved.

Note- In any right angled triangle, the side opposite to the right angle is known as hypotenuse. In this particular problem in order to obtain the LHS of the equation which needs to be proved, Pythagoras theorem is applied in the right triangle ADE and then all the other sides except AD are converted in terms of side A