Question

In a triangle PQR, P is the largest angle and $ \cos P=\dfrac{1}{3} $ . Further the incircle of the triangle touches the sides PQ, QR and RP at N, L and M respectively, such that the lengths of PN, QL and RM are consecutive even integers. Then possible length(s) of the side(s) of the triangle is (are)
(a) 16
(b) 18
(c) 24
(d) 22

Answer 1

Hint:
We start solving the problem by assuming the lengths of PN, QL, and RM. We then draw the figure representing the given information. We then recall the fact that the lengths of the tangents from a point drawn to the circle will be equal to get the length of the sides. We then make use of the cosine law at the angle P and make the necessary calculations to get the value of assumed lengths.

Complete step by step answer:
According to the problem, we are given that P is the largest angle in triangle PQR such that $ \cos P=\dfrac{1}{3} $ . We need to find the possible length(s) of the side(s) of a triangle if the incircle of the triangle touches the sides PQ, QR and RP at N, L and M respectively, such that the lengths of PN, QL and RM are consecutive even integers.
Let us draw the figure representing the given information.

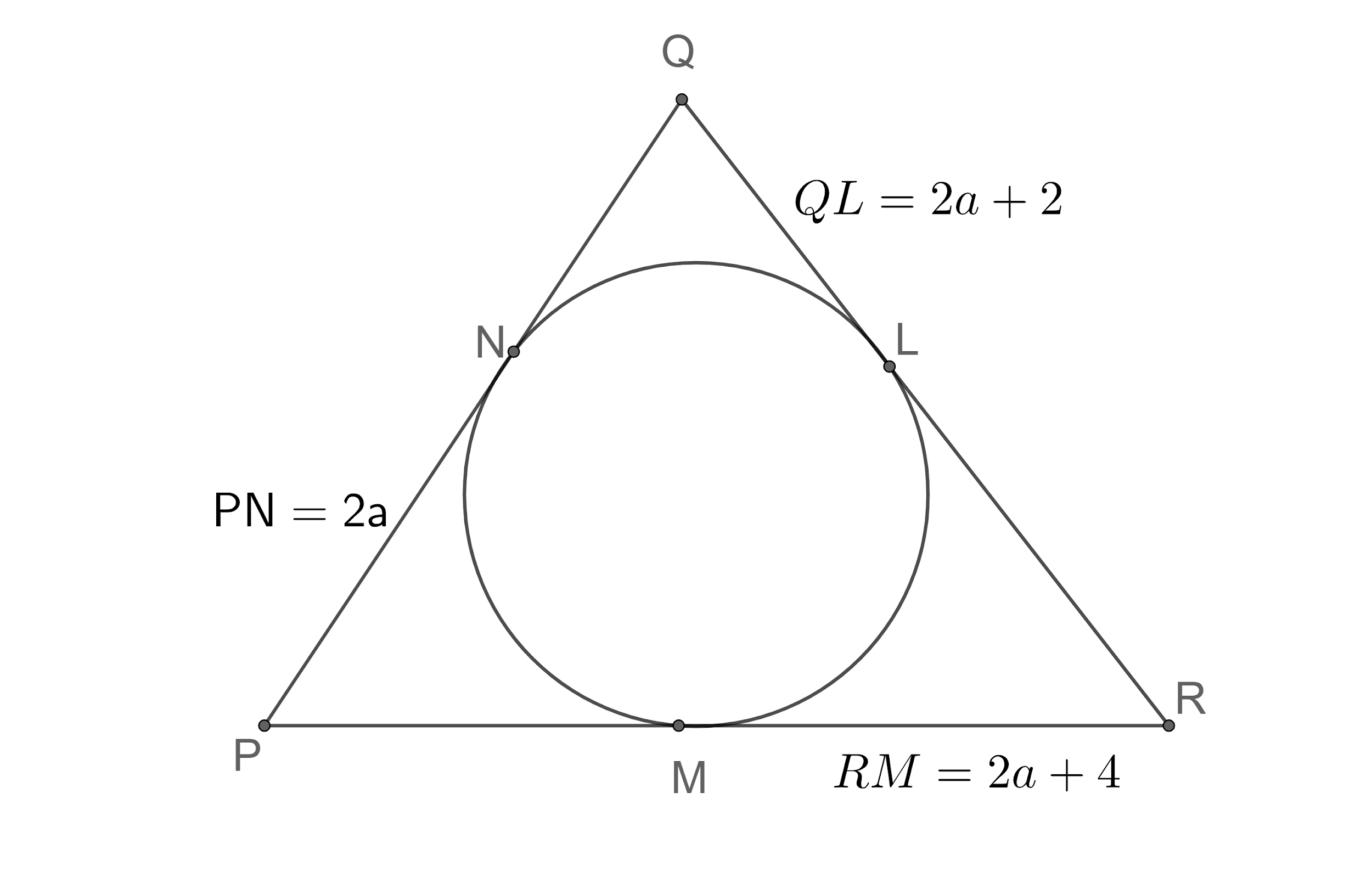
Let us assume the lengths of PN, QL, RM be $ 2a $ , $ 2a+2 $ , $ 2a+4 $ .
We can see that the PN and PM are tangents to the incircle from point P. We know that the length of the tangents from a point draw to the circle will be equal. so, we get $ PN=PM=2a $ .
Similarly, we get $ RM=RL=2a+4 $ and $ QN=QL=2a+2 $ .
Now, let us find the length of the sides PQ, QR, RP.
So, we have $ PQ=PN+NQ=2a+2a+2=4a+2 $ ,
 $ \Rightarrow QR=QL+LR=2a+2+2a+4=4a+6 $ ,
 $ \Rightarrow RP=RM+MP=2a+4+2a=4a+4 $ .
From cosine rule, we know that $ \cos P=\dfrac{P{{R}^{2}}+P{{Q}^{2}}-Q{{R}^{2}}}{2\left( PR \right)\left( PQ \right)} $ .
 $ \Rightarrow \dfrac{1}{3}=\dfrac{{{\left( 4a+4 \right)}^{2}}+{{\left( 4a+2 \right)}^{2}}-{{\left( 4a+6 \right)}^{2}}}{2\left( 4a+4 \right)\left( 4a+2 \right)} $ .
 $ \Rightarrow \dfrac{2}{3}=\dfrac{16{{a}^{2}}+32a+16+16{{a}^{2}}+16a+4-16{{a}^{2}}-48a-36}{16{{a}^{2}}+16a+8a+8} $ .
 $ \Rightarrow \dfrac{2}{3}=\dfrac{16{{a}^{2}}-16}{16{{a}^{2}}+24a+8} $ .
 $ \Rightarrow 32{{a}^{2}}+48a+16=48{{a}^{2}}-48 $ .
 $ \Rightarrow 16{{a}^{2}}-48a-64=0 $ .
 $ \Rightarrow {{a}^{2}}-3a-4=0 $ .
 $ \Rightarrow {{a}^{2}}-4a+a-4=0 $ .
 $ \Rightarrow a\left( a-4 \right)+1\left( a-4 \right)=0 $ .
 $ \Rightarrow \left( a+1 \right)\left( a-4 \right)=0 $ .
 $ \Rightarrow a+1=0 $ , $ a-4=0 $ .
 $ \Rightarrow a=-1 $ , $ a=4 $ .
We neglect the negative value for a, as the length cannot be negative.
So, the value of a is 4.
Now, let us find the length of the sides.
We have $ PQ=4a+2=16+2=18 $ .
 $ \Rightarrow PQ=4a+6=16+6=22 $ .
 $ \Rightarrow RP=4a+4=16+4=20 $ .
So, we have found the possible length(s) of the side(s) of the triangle as 18, 20, 22.
 $ \therefore $ The correct options for the given problem are (b), (d).

Note:
We can see that the given problems contain a huge amount of calculations, so we need to perform each step carefully to avoid confusion. We can also assume the lengths of PN, QL, RM as $ a-2 $ , $ a $ , $ a+2 $ to solve the given problem. We should not confuse incircle with circumcircle or excircle as it will not give us the correct answer. Similarly, we can expect the problems to find the area and perimeter of the triangle using the obtained values of sides.