Question

In a triangle, if the square of one side is equal to the sum of squares of other sides, then the angle opposite to the first side is a right angle. Prove it.

Answer 1

Hint: We prove this statement by considering another triangle which is a right angled triangle and has two sides equal to two sides of the given triangle. Using the Pythagoras theorem in the triangle we constructed, find the value of third side and show both the triangles congruent to each other.
* Pythagoras theorem states that in a right angled triangle, the sum of square of base and square of height is equal to square of the hypotenuse.
If we have a right angled triangle, \[\vartriangle ABC\] with right angle, \[\angle B = {90^ \circ }\]
Then using the Pythagoras theorem we can write that \[A{C^2} = A{B^2} + B{C^2}\]
          

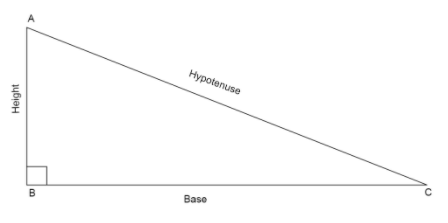
Complete step-by-step answer:
Let us assume a triangle given to us in the question as \[\vartriangle ABC\], which has a square of one side equal to the sum of squares of other sides.
                              

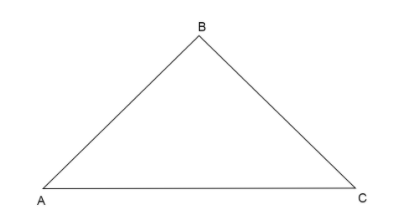
Now we are given for \[\vartriangle ABC\], let the side whose square is equal to the sum of squares of the other two sides be \[AC\]. So, we can write
\[A{C^2} = A{B^2} + B{C^2}\] … (i)
Now we assume another triangle which is a right angle triangle, say \[\vartriangle DEF\] with \[\angle E = {90^ \circ }\] and two sides equal to sides of \[\vartriangle ABC\], say \[AB = DE,BC = EF\]
                              

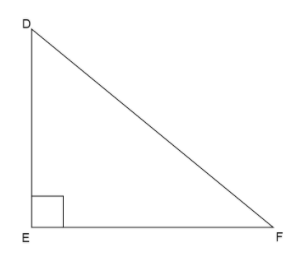
In right angle triangle, \[\vartriangle DEF\], using Pythagoras theorem we can write
Square of hypotenuse is equal to sum of square of base and square of height.
Here, base is \[EF\], height is \[DE\] and hypotenuse is \[DF\].
\[ \Rightarrow D{F^2} = D{E^2} + E{F^2}\] … (ii)
Now we know from equation (i)
\[A{C^2} = A{B^2} + B{C^2}\]
Substitute the values of \[AB = DE,BC = EF\] in equation (i)
\[ \Rightarrow A{C^2} = D{E^2} + E{F^2}\]
But we know from equation (ii) \[ \Rightarrow D{F^2} = D{E^2} + E{F^2}\]
\[ \Rightarrow A{C^2} = D{F^2}\]
Taking square root on both sides of the equation,
\[
   \Rightarrow \sqrt {A{C^2}} = \sqrt {D{F^2}} \\
   \Rightarrow AC = DF \\
 \]
Therefore, now we have all three sides of \[\vartriangle ABC\] equal to three sides of \[\vartriangle DEF\]as
\[
  AB = DE \\
  BC = EF \\
  AC = DF \\
 \]
So, by Side Side Side (SSS) congruence rule, we can say that \[\vartriangle ABC \cong \vartriangle DEF\].
Since, we know two triangles which are congruent have their corresponding sides equal and their corresponding angles equal.
Here, corresponding angles of \[\vartriangle ABC \cong \vartriangle DEF\] are
\[
  \angle A = \angle D \\
  \angle B = \angle E \\
  \angle C = \angle F \\
 \]
So we can say \[\angle B = \angle E = {90^ \circ }\] because \[\angle E = {90^ \circ }\].
Therefore, \[\vartriangle ABC\] is a right angled triangle with \[\angle B = {90^ \circ }\].
Hence Proved.

Note: Students many times make mistake while applying Pythagoras theorem to a right triangle and they write any side on LHS of the equation and other two remaining sides on RHS of the equation which is wrong, the sides whose square we take on one side always has to be the hypotenuse, which can be identified as the side opposite to right angle.