In a triangle ABC, sin A : sin B : sin C =1 : 2 : 3. Find the perimeter of the triangle if b = 4cm.
(a) 6 cm
(b) 24 cm
(c) 12 cm
(d) 8 cm
Answer
Verified360.6k+ views
Hint: To find the perimeter, we make use of sine rule, to find the values of a and c. Then we can calculate the perimeter of the triangle by adding a, b and c.
Complete step-by-step answer:
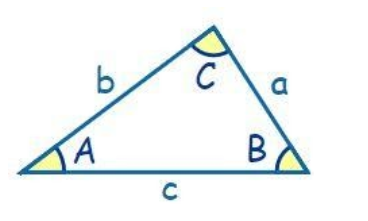
To explain further now, we will refer to the triangle above. The sides a, b and c represent the sides opposite angles A, B and C (as shown in the triangle above). In the question, we are already given that b = 4cm. Thus, all we have to do is calculate the value of a and c.
To do so, we use the sine rule. By sine rule, we have,
$\dfrac{a}{\sin A}=\dfrac{b}{\sin B}=\dfrac{c}{\sin C}=k$
Thus, we have,
a=k$\sin A$ -- (1)
b=k$\sin B$-- (2)
c=k $\sin C$-- (3)
From the question, we also have,
$\sin A:\sin B:\sin C$=1:2:3
Thus, $\dfrac{\sin A}{\sin B}=\dfrac{1}{2}$
Also,
$\begin{align}
& \dfrac{\sin B}{\sin C}=\dfrac{2}{3} \\
& \dfrac{\sin C}{\sin B}=\dfrac{3}{2} \\
\end{align}$
We will use these results in the below calculations-
Now, we divide (1) by (2), we get,
$\begin{align}
& \dfrac{a}{b}=\dfrac{\sin A}{\sin B} \\
& a=b\times \dfrac{\sin A}{\sin B} \\
& a=4\times \dfrac{1}{2} \\
& a=2 \\
\end{align}$
Now, we divide (2) by (3), we get,
$\begin{align}
& \dfrac{b}{c}=\dfrac{\sin B}{\sin C} \\
& c=b\times \dfrac{\sin C}{\sin B} \\
& c=4\times \dfrac{3}{2} \\
& c=6 \\
\end{align}$
Now, since we have the values of a, b and c. We are now ready to calculate the perimeter of the triangle. Thus,
Perimeter = a+b+c
Perimeter = 2+4+6
Perimeter = 12 cm
Hence, the correct answer is (c) 12 cm.
Note: Although not mentioned in the question, as a general rule, it is important to remember that a, b and c are sides to the angles A, B and C respectively. Further, to get the intuition of using sine rule, one can get a hint of this from the sine ratios of various angles given in the question. Whenever such a ratio is given, it is always better to use the sine rule to solve the problem.
Complete step-by-step answer:
To explain further now, we will refer to the triangle above. The sides a, b and c represent the sides opposite angles A, B and C (as shown in the triangle above). In the question, we are already given that b = 4cm. Thus, all we have to do is calculate the value of a and c.
To do so, we use the sine rule. By sine rule, we have,
$\dfrac{a}{\sin A}=\dfrac{b}{\sin B}=\dfrac{c}{\sin C}=k$
Thus, we have,
a=k$\sin A$ -- (1)
b=k$\sin B$-- (2)
c=k $\sin C$-- (3)
From the question, we also have,
$\sin A:\sin B:\sin C$=1:2:3
Thus, $\dfrac{\sin A}{\sin B}=\dfrac{1}{2}$
Also,
$\begin{align}
& \dfrac{\sin B}{\sin C}=\dfrac{2}{3} \\
& \dfrac{\sin C}{\sin B}=\dfrac{3}{2} \\
\end{align}$
We will use these results in the below calculations-
Now, we divide (1) by (2), we get,
$\begin{align}
& \dfrac{a}{b}=\dfrac{\sin A}{\sin B} \\
& a=b\times \dfrac{\sin A}{\sin B} \\
& a=4\times \dfrac{1}{2} \\
& a=2 \\
\end{align}$
Now, we divide (2) by (3), we get,
$\begin{align}
& \dfrac{b}{c}=\dfrac{\sin B}{\sin C} \\
& c=b\times \dfrac{\sin C}{\sin B} \\
& c=4\times \dfrac{3}{2} \\
& c=6 \\
\end{align}$
Now, since we have the values of a, b and c. We are now ready to calculate the perimeter of the triangle. Thus,
Perimeter = a+b+c
Perimeter = 2+4+6
Perimeter = 12 cm
Hence, the correct answer is (c) 12 cm.
Note: Although not mentioned in the question, as a general rule, it is important to remember that a, b and c are sides to the angles A, B and C respectively. Further, to get the intuition of using sine rule, one can get a hint of this from the sine ratios of various angles given in the question. Whenever such a ratio is given, it is always better to use the sine rule to solve the problem.
Last updated date: 20th Sep 2023
•
Total views: 360.6k
•
Views today: 10.60k
