Question

In a triangle ABC, N is appointed on AC such that BN is perpendicular to AC. If $B{N^2} = AN \cdot NC$, prove that $\angle B = {90^0}$.

Answer 1

Hint: - Use Pythagoras Theorem, $\left[ {{{\left( {{\text{Hypotenuse}}} \right)}^2} = {{\left( {{\text{Perpendicular}}} \right)}^2} + {{\left( {{\text{Base}}} \right)}^2}} \right]$

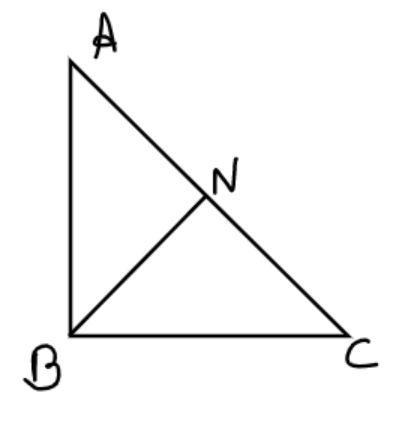
Given:
BN is perpendicular to AC
\[\therefore \angle BNC = \angle BNA = 90\]
And it is also given that $B{N^2} = AN \cdot NC............\left( 1 \right)$
Apply Pythagoras Theorem in $\Delta BNC$
$\therefore {\left( {BC} \right)^2} = {\left( {BN} \right)^2} + {\left( {NC} \right)^2}$
From equation 1
${\left( {BC} \right)^2} = \left( {AN \times NC} \right) + {\left( {NC} \right)^2}.................\left( 2 \right)$
Apply Pythagoras Theorem in $\Delta BNA$
$\therefore {\left( {BA} \right)^2} = {\left( {BN} \right)^2} + {\left( {NA} \right)^2}$
From equation 1
$\therefore {\left( {BA} \right)^2} = \left( {AN \times NC} \right) + {\left( {NA} \right)^2}.........\left( 3 \right)$
Add equations 2 and 3
$
  {\left( {BC} \right)^2} + {\left( {BA} \right)^2} = \left( {AN \times NC} \right) + {\left( {NC} \right)^2} + \left( {AN \times NC} \right) + {\left( {NA} \right)^2} \\
  \therefore {\left( {BC} \right)^2} + {\left( {BA} \right)^2} = {\left( {NC} \right)^2} + {\left( {NA} \right)^2} + 2\left( {AN \times NC} \right) \\
$
In above equation R.H.S is the formula of ${\left( {a + b} \right)^2} = {a^2} + {b^2} + 2ab$
$\therefore {\left( {BC} \right)^2} + {\left( {BA} \right)^2} = {\left( {AN + NC} \right)^2}$
From figure $AN + NC = AC$
$\therefore {\left( {BC} \right)^2} + {\left( {BA} \right)^2} = {\left( {AC} \right)^2}$
Which is the property of Pythagoras Theorem.
Where AC is hypotenuse, AB and BC are perpendicular to each other at B.
$\therefore \angle B = {90^0}$
Hence Proved.

Note: - whenever we face such types of problems first draw the pictorial representation of the given problem, then apply Pythagoras Theorem which is stated above, then according to given condition simplify the problem, then we will get the required answer.