
In a triangle ABC, $a = 7,b = 8,c = 9$, BD is the median and BE is the altitude from the vertex B, then
List – I List – II BD 7 BE 2 BD $\sqrt {35} $ $\sqrt {45} $
The correct match for LIST – I from LIST – II
1) A – 2, B – 1, C – 4
2) A – 3, B – 4, C – 2
3) A – 1, B – 3, C – 2
4) A – 1, B – 4, C – 2
| List – I | List – II |
| BD | 7 |
| BE | 2 |
| BD | $\sqrt {35} $ |
| $\sqrt {45} $ |
Answer
554.7k+ views
Hint: First draw the diagram based on the question. Then, use the cosine formula in $\Delta ABC$ and $\Delta ABD$ and compare the values to get the value of BD. After that use the properties of the isosceles triangle to get the value of ED. Then use the Pythagoras theorem in $\Delta BED$ to get the value of BE.
Complete step-by-step solution:
The diagram of the above equation is,
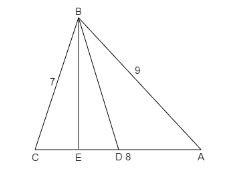
In $\Delta ABC$, the cosine formula for A is given by,
$\cos A = \dfrac{{{b^2} + {c^2} - {a^2}}}{{2bc}}$
Substitute the values,
$ \Rightarrow \cos A = \dfrac{{{8^2} + {9^2} - {7^2}}}{{2 \times 8 \times 9}}$
Simplify the terms,
$ \Rightarrow \cos A = \dfrac{{64 + 81 - 49}}{{144}}$
Add and subtract the terms in the numerator,
$ \Rightarrow \cos A = \dfrac{{96}}{{144}}$
Cancel out the common terms,
$ \Rightarrow \cos A = \dfrac{2}{3}$.............….. (1)
In $\Delta ABD$, the cosine formula for A is given by,
$\cos A = \dfrac{{A{B^2} + A{D^2} - B{D^2}}}{{2 \times AB \times AD}}$
Substitute the values,
$ \Rightarrow \cos A = \dfrac{{{9^2} + {4^2} - B{D^2}}}{{2 \times 9 \times 4}}$
Simplify the terms,
$ \Rightarrow \cos A = \dfrac{{81 + 16 - B{D^2}}}{{72}}$
Add and subtract the terms in the numerator,
$ \Rightarrow \cos A = \dfrac{{97 - B{D^2}}}{{72}}$................….. (2)
Compare the equation (1) and (2),
$ \Rightarrow \dfrac{{97 - B{D^2}}}{{72}} = \dfrac{2}{3}$
Cross-multiply the terms,
$ \Rightarrow 291 - 3B{D^2} = 144$
Move constant part on one side,
$ \Rightarrow 3B{D^2} = 291 - 144$
Subtract the values,
$ \Rightarrow 3B{D^2} = 147$
Divide both sides by 3,
$ \Rightarrow B{D^2} = 49$
Take the square root on both sides,
$\therefore BD = 7$
In $\Delta BCD$, $BC = 7$ and $BD = 7$.
So, $\Delta BCD$ is an isosceles triangle.
We know that the altitude on the non-equal side of the isosceles triangle is the perpendicular bisector. So,
$ \Rightarrow CE = ED$...................….. (3)
The length of the CD is 4. Then,
$ \Rightarrow CE + ED = 4$
Substitute the value from equation (3),
$ \Rightarrow ED + ED = 4$
Add the terms,
$ \Rightarrow 2ED = 4$
Divide both sides by 2,
$\therefore ED = 2$
In $\Delta BED$, apply Pythagoras theorem,
$B{E^2} = B{D^2} - E{D^2}$
Substitute the values,
$ \Rightarrow B{E^2} = {7^2} - {2^2}$
Simplify the terms,
$ \Rightarrow B{E^2} = 49 - 4$
Subtract the values,
$ \Rightarrow B{E^2} = 45$
Take the square root on both sides,
$\therefore BE = \sqrt {45} $
Hence, option (4) is correct.
Note: A line segment drawn from the vertex of a triangle on the opposite side of a triangle which is perpendicular to it is said to be the altitude of a triangle.
A median of a triangle is a line segment joining a vertex to the midpoint of the opposite side, thus bisecting that side.
Complete step-by-step solution:
The diagram of the above equation is,

In $\Delta ABC$, the cosine formula for A is given by,
$\cos A = \dfrac{{{b^2} + {c^2} - {a^2}}}{{2bc}}$
Substitute the values,
$ \Rightarrow \cos A = \dfrac{{{8^2} + {9^2} - {7^2}}}{{2 \times 8 \times 9}}$
Simplify the terms,
$ \Rightarrow \cos A = \dfrac{{64 + 81 - 49}}{{144}}$
Add and subtract the terms in the numerator,
$ \Rightarrow \cos A = \dfrac{{96}}{{144}}$
Cancel out the common terms,
$ \Rightarrow \cos A = \dfrac{2}{3}$.............….. (1)
In $\Delta ABD$, the cosine formula for A is given by,
$\cos A = \dfrac{{A{B^2} + A{D^2} - B{D^2}}}{{2 \times AB \times AD}}$
Substitute the values,
$ \Rightarrow \cos A = \dfrac{{{9^2} + {4^2} - B{D^2}}}{{2 \times 9 \times 4}}$
Simplify the terms,
$ \Rightarrow \cos A = \dfrac{{81 + 16 - B{D^2}}}{{72}}$
Add and subtract the terms in the numerator,
$ \Rightarrow \cos A = \dfrac{{97 - B{D^2}}}{{72}}$................….. (2)
Compare the equation (1) and (2),
$ \Rightarrow \dfrac{{97 - B{D^2}}}{{72}} = \dfrac{2}{3}$
Cross-multiply the terms,
$ \Rightarrow 291 - 3B{D^2} = 144$
Move constant part on one side,
$ \Rightarrow 3B{D^2} = 291 - 144$
Subtract the values,
$ \Rightarrow 3B{D^2} = 147$
Divide both sides by 3,
$ \Rightarrow B{D^2} = 49$
Take the square root on both sides,
$\therefore BD = 7$
In $\Delta BCD$, $BC = 7$ and $BD = 7$.
So, $\Delta BCD$ is an isosceles triangle.
We know that the altitude on the non-equal side of the isosceles triangle is the perpendicular bisector. So,
$ \Rightarrow CE = ED$...................….. (3)
The length of the CD is 4. Then,
$ \Rightarrow CE + ED = 4$
Substitute the value from equation (3),
$ \Rightarrow ED + ED = 4$
Add the terms,
$ \Rightarrow 2ED = 4$
Divide both sides by 2,
$\therefore ED = 2$
In $\Delta BED$, apply Pythagoras theorem,
$B{E^2} = B{D^2} - E{D^2}$
Substitute the values,
$ \Rightarrow B{E^2} = {7^2} - {2^2}$
Simplify the terms,
$ \Rightarrow B{E^2} = 49 - 4$
Subtract the values,
$ \Rightarrow B{E^2} = 45$
Take the square root on both sides,
$\therefore BE = \sqrt {45} $
Hence, option (4) is correct.
Note: A line segment drawn from the vertex of a triangle on the opposite side of a triangle which is perpendicular to it is said to be the altitude of a triangle.
A median of a triangle is a line segment joining a vertex to the midpoint of the opposite side, thus bisecting that side.
Recently Updated Pages
Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Master Class 9 English: Engaging Questions & Answers for Success

Trending doubts
Which places in India experience sunrise first and class 9 social science CBSE

Which is the largest Gulf in the world A Gulf of Aqaba class 9 social science CBSE

Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Write the 6 fundamental rights of India and explain in detail

Difference Between Plant Cell and Animal Cell

What is pollution? How many types of pollution? Define it




