Question

In a right-angled triangle, five times the square on the hypotenuse is equal to four times the sum of the squares on the medians drawn from the acute angles. Prove it.

Answer 1

Hint: In a right-angled triangle, as the Pythagoras theorems say, ${h^2} = {p^2} + {b^2}$, where h is the hypotenuse of a right-angle triangle, p is the perpendicular and b is the base.

Complete step-by-step answer:
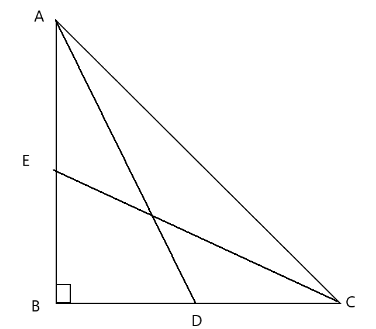
Consider a right angle triangle, $\vartriangle ABC$

In $\vartriangle ABC$, using Pythagoras theorem, ${h^2} = {p^2} + {b^2}$, where h is the hypotenuse of a right-angle triangle, p is the perpendicular and b is the base.
$A{C^2} = A{B^2} + B{C^2}$
Let AB=x and BC=y
$ \Rightarrow A{C^2} = {x^2} + {y^2}$

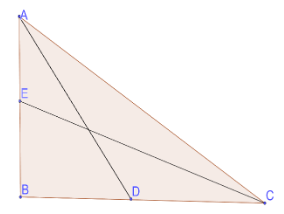
AD and CE are the median drawn from A and B respectively.
 Now, further applying Pythagoras theorem in $\vartriangle ABD$, we get
$
  A{D^2} = {x^2} + {\left( {\dfrac{y}{2}} \right)^2} \\
   \Rightarrow AD = \sqrt {{x^2} + {{\left( {\dfrac{y}{2}} \right)}^2}} \\
$
Similarly, In $\vartriangle ECB$,
$
  C{E^2} = {y^2} + {(\dfrac{x}{2})^2} \\
   \Rightarrow CE = \sqrt {{y^2} + {{(\dfrac{x}{2})}^2}} \\
 $
Now, the sum of the squares of the medians is
$
   \Rightarrow A{D^2} + C{E^2} = {x^2} + {\left( {\dfrac{y}{2}} \right)^2} + {y^2} + {\left( {\dfrac{x}{2}} \right)^2} \\
   \Rightarrow A{D^2} + C{E^2} = \dfrac{5}{4}({x^2} + {y^2}) \\
   \Rightarrow 4\left( {A{D^2} + C{E^2}} \right) = 5({x^2} + {y^2}) \\
$
As, we know $A{C^2} = {x^2} + {y^2}$
$ \Rightarrow 4(A{D^2} + C{E^2}) = 5A{C^2}$
Hence, five times the square on the hypotenuse is equal to four times the sum of the squares on the medians drawn from the acute angles

Note: The Median joins the vertex to the midpoint of the opposite side. The properties of the median are as follows:-
The median divides the triangle into two parts of equal area.
The point of concurrency of medians is called Centroid.
The centroid divides the median in the ratio 2:1 with the larger parts toward the vertex.