Question

In a right-angled triangle ABC which has right angle at B. A circle is drawn with AB as diameter intersecting the hypotenuse at P. Prove that the tangent to the circle at P bisects BC.

Answer 1

Hint: We first draw the information given for us. We can see that side BC is tangent to the circle from a point where tangent P is also passing. We use the fact that angles opposite to equal sides are also equal, sum of angles in a straight line is $ {{180}^{o}} $ to prove the required result.

Complete step-by-step answer:
Given that we have a right-angled triangle ABC whose right angle is at vertex B and we have a circle drawn with AB as diameter intersecting the hypotenuse at P and a tangent is drawn to circle at point P. We need to prove that this tangent bisects the side BC.
Let us draw a figure so that all the information can be viewed better. We assume the tangent of circle at point P intersects side BC at point ‘F’. According to the problem we need to prove BF=FC.

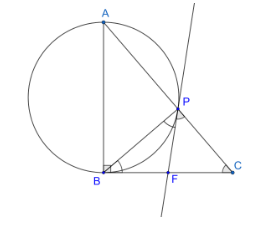
We join the points B and P. We know that the normal of any circle passes through the center of the circle and lies perpendicular to the tangents.
So, we can see that the side BC is perpendicular to the diameter AB. So, side BC satisfies the condition of becoming tangent.
We can see that the tangents BC and PF passes through the point F. This makes lines FB and FP are tangents drawn externally from the point F.
We know that if the lengths of the tangents drawn from the external point to the point of contact on the circle are equal. By using this point we get BF = PF ---(1).
We know that sides opposite to the equal sides has equal angles.
So, we get $ \angle PBC=\angle BPF $ ---(2).
From triangle APB, we can see that $ \angle APB={{90}^{o}} $ ---(3).
We know that the sum of angles lie on a straight line constitutes $ {{180}^{o}} $ . Using this fact on side AC, we have
 $ \angle APB+\angle CPB={{180}^{o}} $ .
From equation (3), we have $ \angle APB={{90}^{o}} $ .
 $ {{90}^{o}}+\angle CPB={{180}^{o}} $ .
 $ \angle CPB={{90}^{o}} $ ---(4).
From triangle BPC we know that sum of angles in a triangle is $ {{180}^{o}} $ ,
 $ \angle PBC+\angle CPB+\angle BCP={{180}^{o}} $ .
From equation (4),
 $ \angle PBC+{{90}^{0}}+\angle BCP={{180}^{o}} $ .
 $ \angle PBC+\angle BCP={{90}^{o}} $ .
From (2), we got
 $ \angle BPF+\angle BCP={{90}^{o}} $ ---(5).
We know that $ \angle CPB={{90}^{o}} $ ,
 $ \angle CPF+\angle BPF={{90}^{o}} $ .
 $ \angle BPF={{90}^{o}}-\angle CPF $ ---(6).
Substituting equation (6) in equation (5) we get,
 $ {{90}^{o}}-\angle CPF+\angle BCP={{90}^{0}} $ .
 $ \angle BCP={{90}^{0}}-{{90}^{o}}+\angle CPF $ .
 $ \angle BCP=\angle CPF $ ---(7).
The sides opposite to angles $ \angle BCP,\angle CPF $ are PF, CF which are also equal.
So, we got PF=CF ---(8)
From equations (1) and (8), we got BF=CP.
∴ We proved that the tangent PF bisects the side BC.

Note: We should not directly take the value of the angle $ \angle PFB $ as $ {{90}^{o}} $ , as the value of the angle will not be the same. We should know that the normal of the circle will always be perpendicular to the tangent and passes through the center of the circle. Here the angle $ \angle APB $ is $ {{90}^{o}} $ , as the angle between the lines connecting both ends of a semicircle is $ {{90}^{o}} $ .