Question

In a right – angled triangle, the sided are $a,b\text{ and }c,$ with $c$ as hypotenuse and
$c-b\ne 1,c+b\ne 1.$ Then the value of $\dfrac{\left( {{\log }_{c+b}}a+{{\log }_{c-b}}a \right)}{\left(
2{{\log }_{c+b}}a\times {{\log }_{c-b}}a \right)}$
A. $2$
B. $-1$
C. $\dfrac{1}{2}$
D. $1$

Answer 1

Hint: Use ${{\log }_{a}}b=\dfrac{1}{{{\log }_{b}}a}$ and basic formula of right angle
 triangle.

As we have given that $a,b\text{ and }c$are sides of right – angled triangle with $c$ as
hypotenuse.

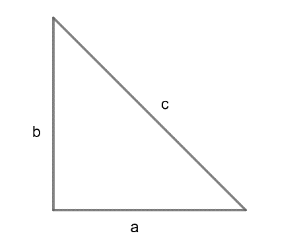
By Pythagoras theorem:
${{c}^{2}}={{b}^{2}}+{{a}^{2}}..........\left( i \right)$
The given expression of which we need to find value is:
$\begin{align}
& =\dfrac{{{\log }_{c+b}}a+{{\log }_{c-b}}a}{2{{\log }_{c+b}}a\times {{\log }_{c-b}}a} \\
& =\dfrac{{{\log }_{c+b}}a}{2{{\log }_{c+b}}a\times {{\log }_{c-b}}a}+\dfrac{{{\log
 }_{c-b}}a}{2{{\log
}_{c+b}}a\times {{\log }_{c-b}}a} \\
& =\dfrac{1}{2{{\log }_{c-b}}a}+\dfrac{1}{2{{\log }_{c+b}}a} \\
& =\dfrac{1}{2}\left( {{\log }_{a}}\left( c-b \right)+{{\log }_{a}}\left( c+b \right)
 \right)\text{
}\because \left( {{\log }_{a}}b=\dfrac{1}{{{\log }_{b}}a} \right) \\
& =\dfrac{1}{2}{{\log }_{a}}\left( c-b \right)\left( c+b \right)\text{ }\because \left(
{{\log }_{x}}a+{{\log }_{x}}b={{\log }_{x}}ab \right) \\
& =\dfrac{1}{2}{{\log }_{a}}{{c}^{2}}-{{b}^{2}}.................\left( ii \right) \\
\end{align}$
From the equation (i)
${{c}^{2}}={{b}^{2}}+{{a}^{2}}$
Hence, equation (ii) will become

$\begin{align}
& =\dfrac{1}{2}lo{{a}_{a}}{{a}^{2}} \\
& =\dfrac{2}{2}{{\log }_{a}}a\text{ }\left( {{\log }_{x}}{{a}^{n}}=n{{\log }_{x}}a \right) \\
& ={{\log }_{a}}a \\
& =1 \\
\end{align}$
Hence, option D is the correct answer.
Note: (i) One need to remember the basic formula between logarithmic functions as used in
 the solution for the flexibility which is an important part of the solution with respect to the
 calculation point of view.
(ii) One can change the given expression in following way:
$\begin{align}
& \dfrac{{{\log }_{c+b}}a+{{\log }_{c-b}}a}{2{{\log }_{c+b}}a.{{\log }_{c-b}}a} \\
& =\dfrac{\dfrac{{{\log }_{x}}a}{{{\log }_{x}}\left( c+b \right)}+\dfrac{{{\log }_{x}}a}{{{\log
 }_{x}}\left(
c-b \right)}}{\dfrac{2{{\log }_{x}}a}{{{\log }_{x}}\left( c+b \right)}\times \dfrac{{{\log
 }_{x}}a}{{{\log
}_{x}}\left( c-b \right)}} \\
\end{align}$
As we have formula ${{\log }_{a}}b=\dfrac{{{\log }_{c}}b}{{{\log }_{c}}a}$ with positive $c$.
And simplifying the above expression will also give the answer, but at the end the same
 calculation is required. So no need to change the bases of given logarithm functions. We can
 observe the expression and need to solve in the same way as done in the solution.