In a rectangle XYWZ, suppose O is the point of intersection of its diagonals if $\angle {\text{ZOW}}$ is $110^o$, then calculate the value of $\angle {\text{OYW}}$.
Answer
Verified358.5k+ views
Hint: In order to solve this problem draw a diagram according to the question then use the concept of vertically opposite angles and sum of angles in one round is 360 degrees knowing these two things will solve this problem.
Complete step-by-step answer:
The rectangle XYWZ can be drawn as:
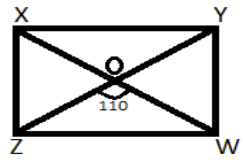
It is given that $\angle {\text{ZOW}}$ is 110 degrees.
We need to find $\angle {\text{OYW}}$.
We know $\angle {\text{YOW}}$+$\angle {\text{OYW}}$+$\angle {\text{OWY}}$= $180^o$ (sum of all three angles in a triangle is 180)
And we can say $\angle {\text{OYW}}$= $\angle {\text{OWY}}$ (Since In triangle OYW sides OY = OW because diagonals of rectangle bisect each other and the lengths of diagonal of rectangle are equal so we know that if the sides are equal in a triangle then angles will be equal)
So the equation becomes $\angle {\text{WOY}}$+2$\angle {\text{OYW}}$= $180^o$ ……(1)
And we know the sum of angles is one round and equals 360 degrees.
So we can say $\angle {\text{XOZ}}$+$\angle {\text{XOY}}$+$\angle {\text{YOW}}$+$\angle {\text{ZOW}}$=360 …..(2)
We can say $\angle {\text{XOZ}}$=$\angle {\text{YOW}}$ (vertically opposite angles)
And also $\angle {\text{XOY}}$= $\angle {\text{ZOW}}$=$110^o$ (given) (vertically opposite angles)
On putting the values in equation 2 we get the value of equation as:
220+2$\angle {\text{YOW}}$=360
$\angle {\text{YOW}}$=$\dfrac{{140}}{2} = 70$
On putting this value in equation 1 we get the equation as:
70+2$\angle {\text{OYW}}$=180
2$\angle {\text{OYW}}$=110
$\angle {\text{OYW}}$=$\dfrac{{110}}{2} = 55^o$
Hence the value of the angle is 55 degrees i.e. $55^o$.
Note: Whenever you face such types of problems drawing diagrams will help you to visualize and solve the problem and will make it a bit easier. Here in this problem we have used the concepts used in angles in triangles like vertically opposite angles and sum of angles in one round is 360 degrees, sum of all three angles in a triangle is 180. Using these concepts will solve this problem.
Complete step-by-step answer:
The rectangle XYWZ can be drawn as:
It is given that $\angle {\text{ZOW}}$ is 110 degrees.
We need to find $\angle {\text{OYW}}$.
We know $\angle {\text{YOW}}$+$\angle {\text{OYW}}$+$\angle {\text{OWY}}$= $180^o$ (sum of all three angles in a triangle is 180)
And we can say $\angle {\text{OYW}}$= $\angle {\text{OWY}}$ (Since In triangle OYW sides OY = OW because diagonals of rectangle bisect each other and the lengths of diagonal of rectangle are equal so we know that if the sides are equal in a triangle then angles will be equal)
So the equation becomes $\angle {\text{WOY}}$+2$\angle {\text{OYW}}$= $180^o$ ……(1)
And we know the sum of angles is one round and equals 360 degrees.
So we can say $\angle {\text{XOZ}}$+$\angle {\text{XOY}}$+$\angle {\text{YOW}}$+$\angle {\text{ZOW}}$=360 …..(2)
We can say $\angle {\text{XOZ}}$=$\angle {\text{YOW}}$ (vertically opposite angles)
And also $\angle {\text{XOY}}$= $\angle {\text{ZOW}}$=$110^o$ (given) (vertically opposite angles)
On putting the values in equation 2 we get the value of equation as:
220+2$\angle {\text{YOW}}$=360
$\angle {\text{YOW}}$=$\dfrac{{140}}{2} = 70$
On putting this value in equation 1 we get the equation as:
70+2$\angle {\text{OYW}}$=180
2$\angle {\text{OYW}}$=110
$\angle {\text{OYW}}$=$\dfrac{{110}}{2} = 55^o$
Hence the value of the angle is 55 degrees i.e. $55^o$.
Note: Whenever you face such types of problems drawing diagrams will help you to visualize and solve the problem and will make it a bit easier. Here in this problem we have used the concepts used in angles in triangles like vertically opposite angles and sum of angles in one round is 360 degrees, sum of all three angles in a triangle is 180. Using these concepts will solve this problem.
Last updated date: 22nd Sep 2023
•
Total views: 358.5k
•
Views today: 10.58k
