Question

In a quadrilateral $ABCD$, $BP$ and $DQ$ are drawn perpendicular to diagonal $AC$ such that $BP = DQ$. If $BR$ equals to $12cm$ where $R$ is the point of intersection of $AC$ and $BD$ then $BD$ is

Answer 1

Hint: In this problem, we have to find the value of the side in the quadrilateral $ABCD$. They give the relation of quadrilateral $ABCD$, by using those given in geometrical relations. We will find the required value of the side. In order to solve this question, we have to $\vartriangle DQR$ and $\vartriangle BPR$ are congruent.

Complete step-by-step answer:

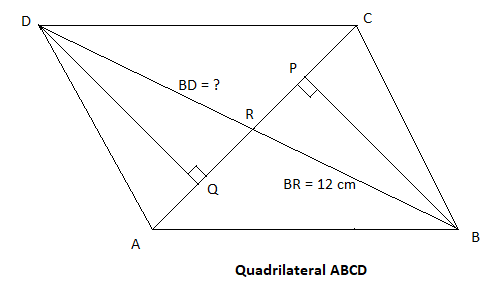
It is stated in the question that $ABCD$ is a quadrilateral in which diagonals $AC$ and $BD$ intersect each other at the point $R$.
It is also given $DQ \bot AC$ and $BP \bot AC$.
Now from the triangle $\vartriangle DQR$ and $\vartriangle BPR$ we get-
$\angle DRQ = \angle BRP$ as they are vertically opposite angles
$\angle DQR = \angle BPR$since each of them is right angle
$BP = DQ$ as mentioned in the question
Therefore $\vartriangle DQR \cong \vartriangle BPR$ since it satisfies the condition of A-A-S of congruency
So, $DR = BR$$ = 12cm$
Thus, $BD = BR + DR = 12 + 12 = 24cm$

Hence the value of $BD$ is equals to $24cm$

Note: When all the three sides and three angles of the two triangles are equal then the two triangles can be said to be congruent.
The main conditions for congruency are given below:
If all the sides of one triangle are equal to all the three sides of the other triangle, then the two triangles are said to be congruent.
If two sides of a triangle and the angle present between them is equal to the other two sides and angle present between them of another triangle, then the two triangles are regarded as congruent.
If any two angles and a side of a triangle is equal to the two angles and one side of the other triangle, then the two triangles are said to be congruent.
If the hypotenuse and a side of a right- angled triangle is equivalent to the hypotenuse and a side of the second right- angled triangle, then the two right triangles are said to be congruent by RHS rule.