Question

In a marriage ceremony of her daughter Poonam, Ashok has to make arrangements for the accommodation of 150 persons. For this purpose, he plans to build a conical tent in such a way that each person have $ 4\;{\text{sq}}{\text{.}}\,{\text{meters}} $ of the space on ground and $ 20\;{\text{cubic}}\;{\text{meters}} $ of air to breath. What would be the height of the conical tent?
A. $ 20\;{\text{m}} $
B. $ 15\;{\text{m}} $
C. $ 12\;{\text{m}} $
D. $ 30\;{\text{m}} $

Answer 1

Hint: To solve the given problem, first of all we will have to find the area of the tent for the 150 people as the area for each person is given. Then we will have to find the volume for 150 people as for the person it is given. Then by using the formula of volume of cone we can find the height of the conical tent.

Complete step-by-step answer:
Given:
The total number of people in the ceremony is $ 150 $ .
The space required on the ground for each person is $ 4\;{\text{sq}}{\text{.}}\;{\text{meters}} $ .
Volume of air required by one person is $ 20\;{\text{cubic}}\;{\text{meters}} $ .
The following is the schematic diagram of the conical tent.

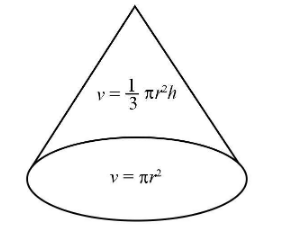
For the conical tent, the area of the base of the tent will be,
 $
\Rightarrow A = 150 \times 4\;{\text{sq}}{\text{.}}\;{\text{meters}}\\
\Rightarrow A = 600\;{\text{sq}}{\text{.}}\,\;{\text{meters}}
 $
The formula for the area of the base of the cone is $ \pi {r^2} $ .
Therefore, \[\pi {r^2} = 600\;{\text{sq}}{\text{.}}\;{\text{meters}}\].
 So, the above expression of area can be written as:
 $
{r^2} = \dfrac{{600\;{\text{sq}}{\text{.}}\;{\text{meters}}}}{\pi }\\
{r^2} = \dfrac{{2100}}{{11}}\;{\text{sq}}{\text{.}}\;{\text{meters}}
 $
Volume of air required by 150 people will be,
 $ v = 150 \times 20\;{\text{cubic meters}} = 3000\;{\text{cubic meters}} $
The formula for the volume of cone is $ v = \dfrac{1}{3}\pi {r^2}h $ .
Substitute $ 3000\;{\text{cubicmeters}} $ for $ v $ and $ \dfrac{{2100}}{{11}}\;{\text{sq}}{\text{.}}\;{\text{meters}} $ for $ {r^2} $ in the above expressions.
 $ 3000\;{\text{cubic meters}} = \dfrac{1}{3}\pi \times \dfrac{{2100}}{{11}}\;{\text{sq}}{\text{.}}\;{\text{meters}} \times h $
Rearrange the above expression.
 $
\Rightarrow h=\dfrac{{3000\;{\text{cubic meters}}}}{{\dfrac{1}{3}\pi \times \dfrac{{2100}}{{11}}\;{\text{sq}}{\text{.}}\;{\text{meters}}}}\\
h=\dfrac{{3000}}{{\dfrac{1}{3} \times \dfrac{{22}}{7} \times \dfrac{{2100}}{{11}}}}{\text{meters}}\\
h = 15\;{\text{meters}}
 $
Hence, the height of the conical tent will be $ 15\;{\text{m}} $ .
So, the correct answer is “Option B”.

Note: In the question, the data is given for each person, so make sure to calculate the data for the 150 people as the total volume occupied will be the volume occupied by 150 people. The calculations should be done in the standard units only.