Question

In a group of children 35 play football out of which 20 play football only, 22 play hockey; 25 play cricket out of which 11 play cricket only. Out of these 7 play cricket and football but not hockey, 3 play football and hockey but not cricket and 12 play football and cricket both. How many play all the three games?
A. 5
B. 5
C. 12
D. 7

Answer 1

Hint: At first jot down the given data in the question and then try to make Venn diagram and from that Venn diagram use the formula that \[n\left( F\cap C \right)=n\left( F\cap C \right)\left\{ not\text{ hockey} \right\}+n\left( F\cap C\cap H \right)\] to get the answer.

Complete step-by-step answer:
 In the question we are told that there are a total 35 children out of which 20 play football only, 22 play hockey and 25 play cricket out of which 11 play cricket only. Out of these 7 play cricket and football but not hockey, 3 play football and hockey but not cricket and 12 play football and cricket both and now from all the data given we will find a number of children who play all these games.
Let football be considered as F, hockey be as H and cricket as C. So according to the data given we can write,
\[\begin{align}
  & n\left( F\text{ only} \right)=20 \\
 & n\left( H \right)=22 \\
 & n\left( C \right)=25 \\
 & n\left( C\text{ only} \right)=11 \\
 & n\left( C\cap F \right)\left\{ not\text{ hockey} \right\}=7 \\
 & n\left( F\cap H \right)\left\{ not\text{ cricket} \right\}=3 \\
 & n\left( F\cap C \right)=12 \\
 & n\left( F\cap H\cap C \right)=x \\
\end{align}\]
Let’s represent the above written data in Venn diagram:

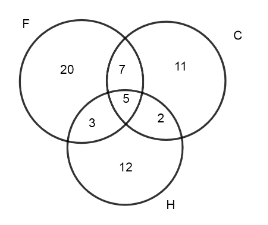
As we were given that \[n\left( F\cap C \right)=12\]
Here are ordering to Venn diagram,
\[n\left( F\cap C \right)=n\left( F\cap C \right)\left\{ not\text{ hockey} \right\}+n\left( F\cap C\cap H \right)\]
So, as we know the values we can substitute them so we get,
\[12=7+x\Rightarrow x=5\]
So, the correct answer is “Option A”.

Note: While solving these kinds of questions students have questions regarding \[n\left( F \right)\text{ and }n\left( F\text{ only} \right)\] as they are both different values. This also goes for \[n\left( C \right)\text{ and }n\left( H \right)\] too.