Question

In a group of 60 people, 27 like cold drinks and 42 like hot drinks and each person likes at least one of the two drinks. How many like both the cold drink and hot drink.

Answer 1

Hint: Take the number of people who like hot and cold drinks as n(H) and n(C) respectively. The number of persons who like both can be written as \[n\left( H\cap C \right)\] and total be as \[n\left( H\cup C \right)\]. Then, use the formula, \[n\left( H\cup C \right)=n\left( H \right)+n\left( C \right)-n\left( H\cap C \right)\] to find the value of \[n\left( H\cap C \right)\].

Complete step-by-step answer:
In the question, we are told about a group of 60 people, where 27 like cold drinks and 42 like hot drinks. It is further said that, each person among 60 people likes at least one of the drinks, so we have to find how many people like both the cold drink and hot drink.
Now, let's consider cold drinks as C and hot drinks as H. So, we can represent, number of persons who like cold drinks as n(C) and number of persons who like hot drinks as n(H) and number of persons who like both of them as \[n\left( H\cap C \right)\] which is to be find out. The total number of persons can be taken as \[n\left( H\cup C \right)\] so, we can write,
\[n\left( H\cup C \right)=n\left( H \right)+n\left( C \right)-n\left( H\cap C \right)\]
Now, we will substitute values of \[n\left( H\cup C \right),n\left( H \right)\text{ and }n\left( C \right)\] to find \[n\left( H\cap C \right)\] so, we get,
\[\begin{align}
  & 60=42+27-n\left( H\cap C \right) \\
 & \Rightarrow n\left( H\cap C \right)=42+27-60 \\
\end{align}\]
Which can be solved as,
\[\begin{align}
  & n\left( H\cap C \right)=69-60 \\
 & \Rightarrow n\left( H\cap C \right)=9 \\
\end{align}\]
So, the total number of people who drink both the hot and cold drink is 9.

Note: We can do the same question by Venn diagram method. Let's consider cold drinks as C and hot drinks as H. Also, let's suppose the number of students who drink both hot and cold drinks is x. So, we can write it as,

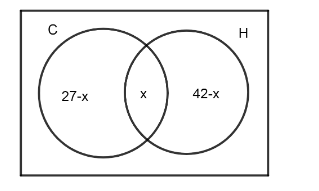
Further, it is said that each person drinks at least one drink and the total number of persons is 60. So, we can say, \[\left( 27-x \right)+x+\left( 42-x \right)=60\] by solving x, we can find what is desired.